[差 3 题][2nd ucup] Warsaw 站选做

本来不想做 ucup 了，但是发现我好像也没有别的题能做（大雾。

比赛链接。

C. Cliques

题意

给定一棵个点的树和一个初始为空的图。

进行次操作，每一次操作为给图加上或删掉一个点，满足。

图上的一个点对应了树的一条路径，图上两个点之间有边，当且仅当其对应的路径在上有公共点。

在每一次操作之后，输出图上有多少个子图是团。

，。

题解

有点脑瘫了哥们。

首先可以知道，两条链的交一定是一条链（可能为空），所以多条链的交也一定是一条链。

那么令的根为，设里一个团的『关键点』为其所有链在中的公共点里，最靠上的一个。

那么考虑直接枚举中的点，计算其是多少个团的关键点。

设有条链经过了这个点，条链同时经过了这个点和他的父亲，那么这个点的贡献是。

带修的话直接上树剖就行，时间复杂度。

提交记录。

G. Matrix Inverse

题意

给定一个矩阵，求出它的逆。

题目额外给出一个矩阵，保证与至多有个位置不同。

。

题解

令为与有多少个位置不同。

首先因为过不了，所以我们甚至无法用矩阵乘法来判两个矩阵是否互为逆。

考虑一个经典 trick，我们随机一个的矩阵，并且计算。

如果的话，那么大概率会有。

否则如果有，那么就一定会有。

同理我们随机一个的矩阵并计算。

此时如果有，那么就一定会有。

这样我们就能确定个不同的位置在哪些行和列，现在我们有个不确定的位置。

考虑这个过程，的第行决定了的第行，而我们知道。

那么我们直接对于的个关键行里面，个关键列拿出来跑高斯消元就好了。

时间复杂度。

提交记录。

K. Jump Graph

题意

给定一个长度为的排列，现在有一张有向图。

图上存在边当且仅当对于每一个都有。

对于每一个点，求出到其他所有点的距离之和。

。

题解

考虑建出这个排列的笛卡尔树（大根）。

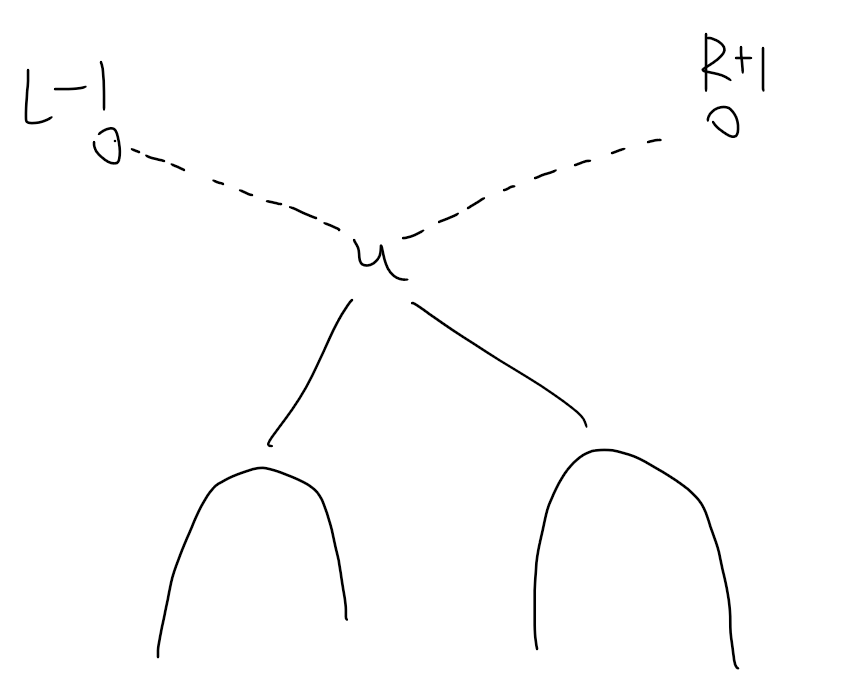
考虑对于一个点，来说，其左子树的点如果想要跳到右子树，那么第一步肯定是跳到或者。

（这是显然的，首先这个点得跳出这个子树，如果要跳出子树就只能往祖先跳，那么显然只会往和，其他的祖先很不优）。

那么考虑先求出每一个点到其子树内点的距离和，但是容易发现这里有一点问题。

假设我们要从点到其右子树内某个点，可能是直接往下走，也有可能是先跳到再往下走，这不好办。

但是我们发现这条双向边是存在的，也就是说对于，有。

那么我们对于每一棵子树维护，以其整个区间的左侧一个极大点为起点，到整棵子树点的距离和是多少。

再额外维护，有多少个点，从左侧极大点的距离比从右侧极大点距离小，有多少个点相等，有多少个点右边小。

这样就能处理出大部分情况了，有少部分情况，子树左侧或右侧不存在极大点，可能需要特殊处理。

再预处理完每一个点到子树内的距离和之后，再递归一遍就能算出每一个点到子树外的距离和了。

时间复杂度。

提交记录。

~~这题感觉写起来真的好煎熬好煎熬~~

B. The Doubling Game 2

题意

给定一棵个点的树，初始的时候每一个节点上都有一个石头。

现在可以进行若干次操作，每一次操作为选定两个相邻节点，满足这两个节点上石头数量相等，然后把一个节点上的所有石头放到另一个节点上。

求最后能形成多少种石头排列的方案。

。

题解

感觉比较神秘啊这个题。

首先可以发现的事情是，一个节点上石头的个数一定是的若干次方。

然后，如果一个点上的石头被挪走了，那么这个节点上之后都不可能出现石头了。

考虑如果最后，某一个节点上有个石头，这些石头是怎么移动的。

首先，这个节点本身有个石头，然后其相连的点里面，依次送来了个石头来合并。

那么这个时候我们就可以考虑进行 dp 了。

设表示子树内部的答案，表示给父亲送恰好个石子的方案数，表示的父亲需要给恰好个石子的方案数。

转移的话，对于每一个点开一个表示已经确定了点的前若干个儿子，现在点已经有的构成了集合的方案数。

同理还有一个表示还缺这些集合的方案数。

直接转移，复杂度是。

观察到一个结论，设表示点上最多可能有多少石子，那么是的。

严谨证明不难，但是好像没有感性一点的证明方式，懒得写了。

直接观察到结论复杂度没什么改进，还是。

考虑对于每一个点，将其所有儿子按照大小升序排序，并且做 dp 的时候第二维只开这么大。

那么显然，一个点在和其父亲合并时，复杂度为，总复杂度为。

提交记录。

H. Inverse Problem

题意

给定一棵个点的树，现在需要给每一个点染一个颜色，颜色共有种。

一种染色方案是合法的，当且仅当对于任意的都有点颜色不同。

给定一个数字，构造一棵树使得染色方案数对取模的结果为。

组数据，时限秒。