赛时拿到高分,赛后和 lrs 花了 1h 推到满分,写题解纪念之。
我也不知道这篇题解怎么这么长。
题目链接
题意
对于一张有 个点, 条边的有向图(边有编号,编号在
之间,可重),我们称它是好的,当且仅当它满足以下条件:
- 对于每一个点,以它为起点的边恰好有 条,且编号为 的各有一个;
- 对于每一个点,以它为终点的边恰好有 条,且编号为 的各有一个;
- 任选一个点
与两种编号 ,设从 出发,先走
边,再走 边到达的点为 ,从 出发,先走 再走 到达的点位 ,都有 。
现给定一张 个点 条边的图,保证他是好的。
你现在需要新建
条边,边的编号在
之间。
求最终这张有
条边的图,有多少种方案是好的。
。
。
。
题解
这道题实在是太难了,我在最终解决它的过程中也使用了一些工具(oeis)。
所以这篇题解主要分为两部分,第一部分根据我的考场思路,讲如何自然地推出
分,第二部分讲如何把 分优化为满分。
本题解中所有的连通均指有向图的弱联通。
基础结论
这道题看起来没有任何切入点,我们不妨从简单的情况看起。
考虑
的时候,整张图长什么样子。
不难发现,此时整张图一定被分为若干个环。
在此基础上,考虑加上编号为
的边,看看图会有什么变化。
假设现在有一个编号为
的边构成的环 ,如下图(黑色表示编号为 的边,红色表示编号为 的边):
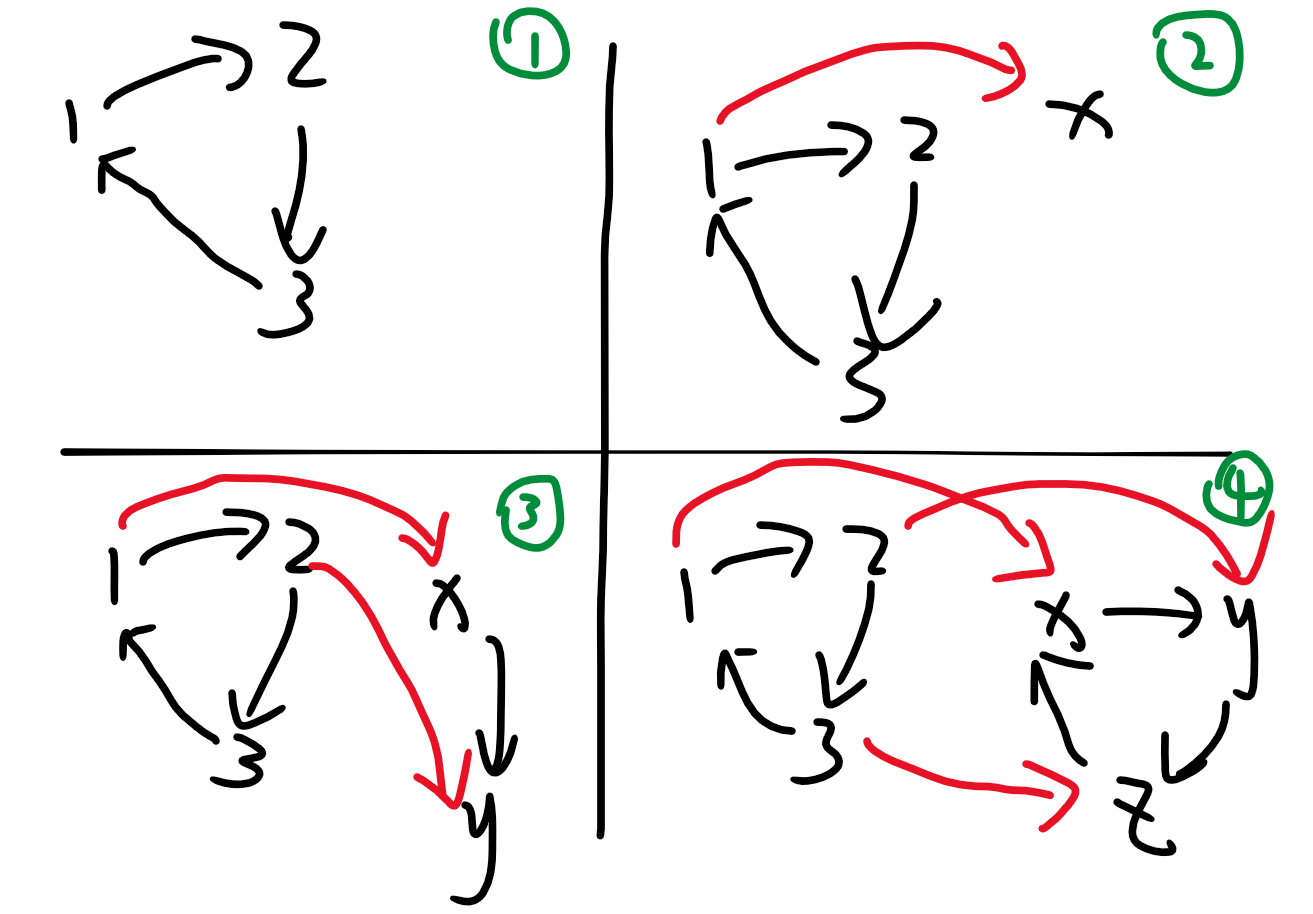
假设 号点连出的 边指向 ,
连出的 边指向 。
那么按照第三条条件,从点 经过
两条边到了 ,那么从 走 两条边也应该走到 。
那么我们就知道, 连出的 边应当指向 。
同理, 连出的 边,与 连出的 边应当指向一个点 。
特殊地,我们还可以推出 连出的
边应当指向点 。
这里可以发现一些规律:
若存在一条 边 ,则 所在的连通块(仅保留前 种边)连出的所有 边,一定在连向 所在的连通块。
入边同理。
证明是简单的,按照我上述的过程进行构造即可,由于不是重点就不展开讲了。
特殊地,我们从上述条件中可以看出,如果在连完一条
边后,两个连通块合并,则两个连通块大小一定相等。
但是,是否所有大小相等的连通块都可以进行连边合并呢?
显然是不行的。
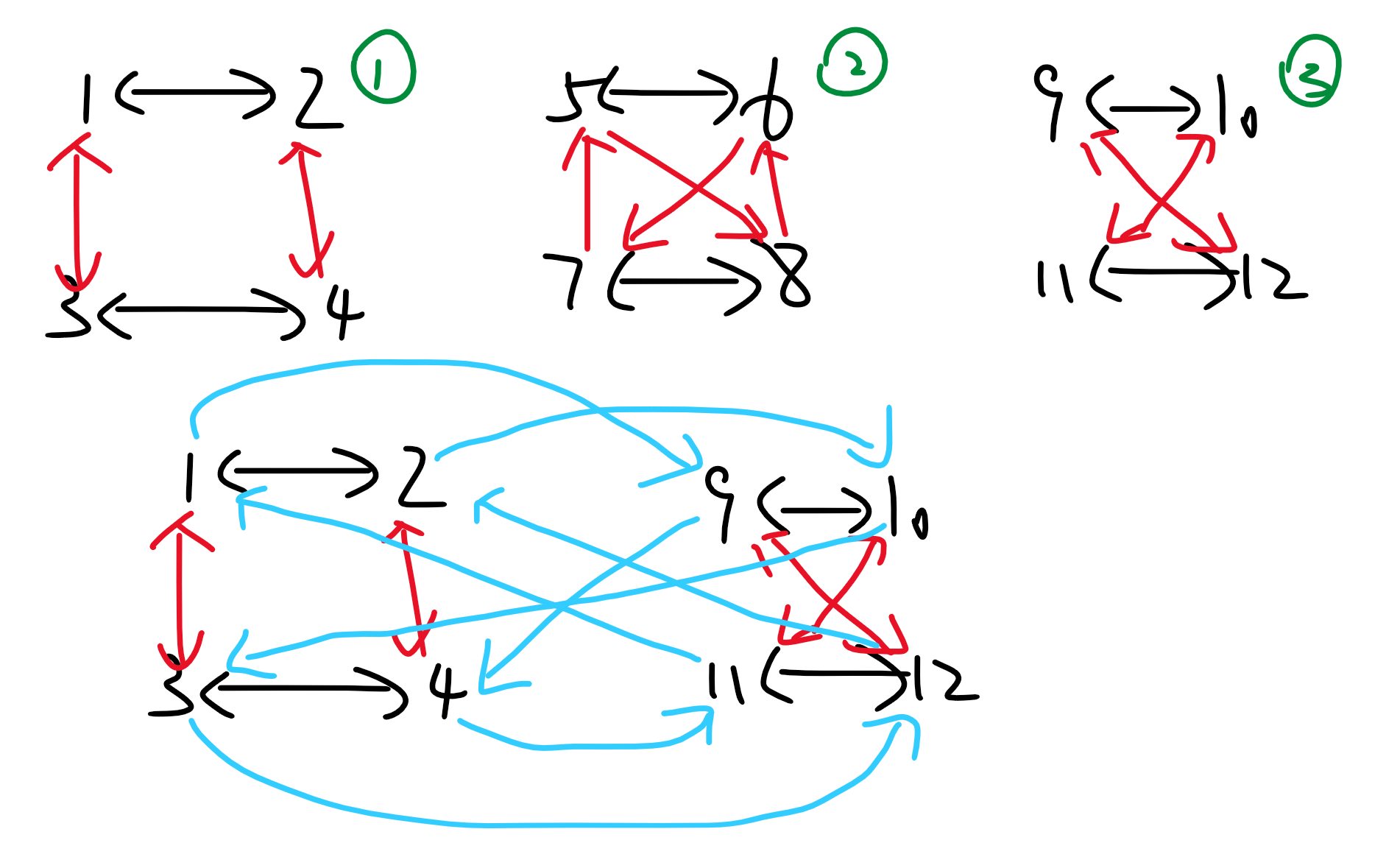
例如上图有
个连通块,每一个连通块大小都是相等的。
但是
两个连通块不能合并,
两个连通块也不能合并(可以自己试试)。
唯一可以合并的是
两个连通块,这里画出了可能的一种合并方式。
为了判断两个连通块能否合并,我们不妨自己进行这样一个定义:
对于两个只存在编号为
的边的连通块 和 ,与点 和 。
若称这两个连通块关于 “同构”,当且仅当:
- 且 ;
- 存在 的排列 使得 ;
- 存在 的排列 使得 ;
- 对于任意节点 ,若从 出发走
边到达了点 ,则从 出发走 边一定到达节点 。
不知道这个名字起的怎么样,我觉得挺顺耳的。
显然,按照我们的定义,有一些显然的结论,例如同构具有传递性。
那么对于任意两个点 ,若他们所在的连通块在连完一条 边 后合法,当且仅当这两个连通块关于 同构。
这个比较简单,就不证了。
比较重要的是下面这个结论:
对于一个连通块 与其中两点
,这个连通块与自己关于
同构。
这个也比较显然,归纳就可以证明。
大题的思路是考虑若干个连通块,在连完一种边后合并在一起的过程。
就可以利用同构的传递性,以及合并连通块需要同构,这两个性质进行证明。
那么还可以推出:
对于两个连通块 与
,若他们关于 同构。
则对于任意两个点
与 ,这两个连通块关于
同构。
这个也好证,结合上一个结论与传递性即可。
从这个结论也可以看出,两个连通块同构,和我们选取的两个点
并没有什么关系(其实选取也只是为了方便证明)。
所以下文的同构,会将这两个点省略,直接说某两个连通块同构。
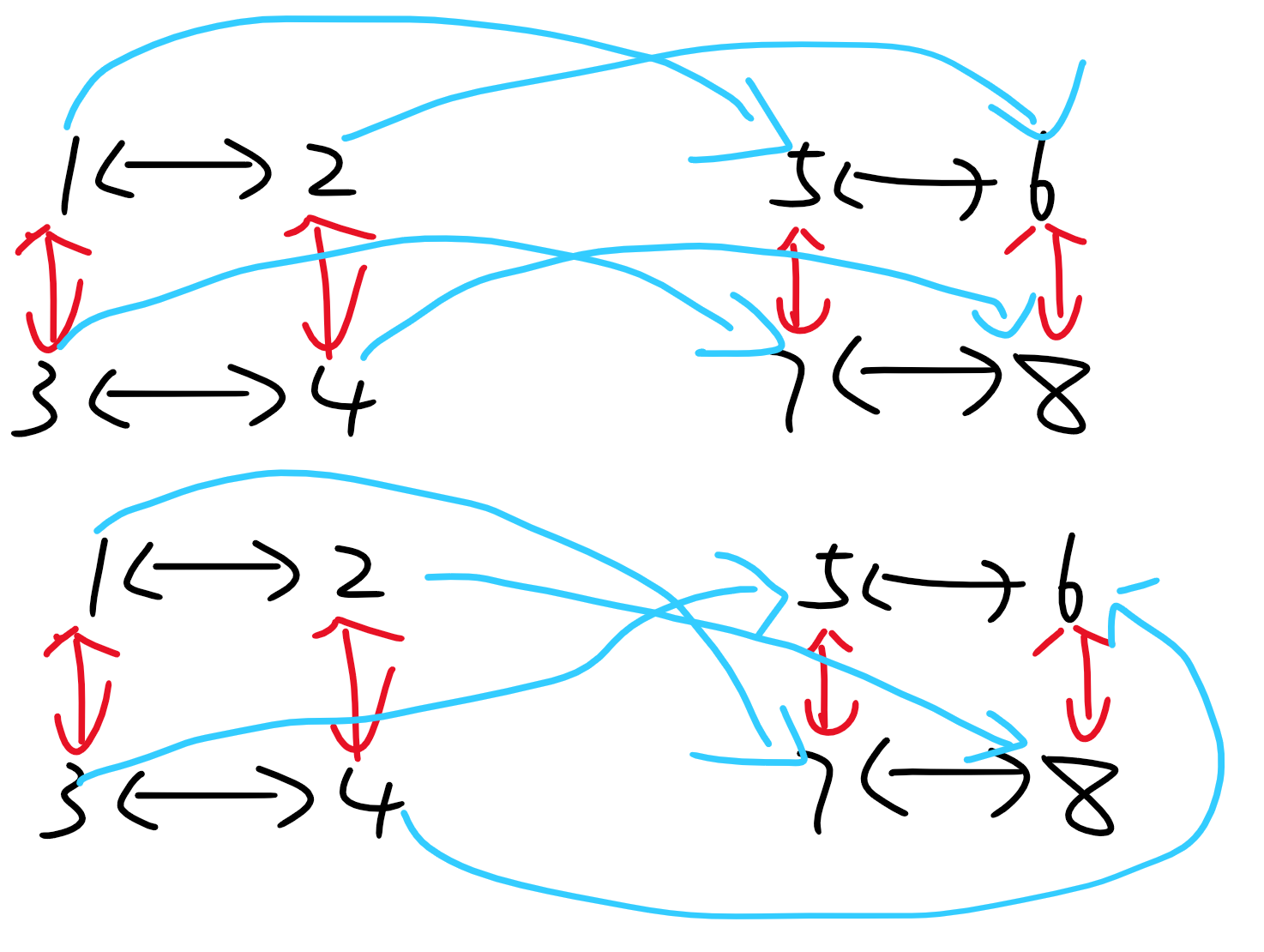
这个结论是很有意思的,这告诉我们,对于两个同构的连通块。
如果我们要从第一个连通块向第二个连通块连边,那么我们只需要确定任何一个点所指向的点,就能唯一确定一个合法方案。
dp 设计
至此,我们就可以尝试进行做法的设计了。
首先考虑输入的图。不难发现,若当前的两个连通块在连完了新的
种边后合并了,则这两个连通块此时同构。
显然,我们可以把所有的连通块分为若干类,其中每一类的所有连通块同构。
那么每一类之间的答案是独立的,我们只需要把它们的答案分别算出,乘起来即可。
而将连通块分类也是简单的,容易使用哈希在 复杂度内完成分类。
现在我们只需要考虑所有连通块都同构的情况了。
设 表示现在有 个同构的连通块,每一个大小都是 ,在连了
种边后,所有点被连进一个连通块的方案数。
所有点被连进一个连通块如果能算出来,那么最终的方案容易使用另一个 dp
算出。
考虑这个状态如何转移。
边界状态是简单的,显然有 。
否则,我们枚举 ,表示第一次连边之后,整张图剩下了 个连通块,那么每一个连通块必然是由
个连通块拼起来的。
那么有转移方程 。
其中 表示将 个连通块分为 个大小相等的圆排列的方案数,容易使用
的 dp 算出。
方程中的
表示连边的方案数,这个需要推一下。
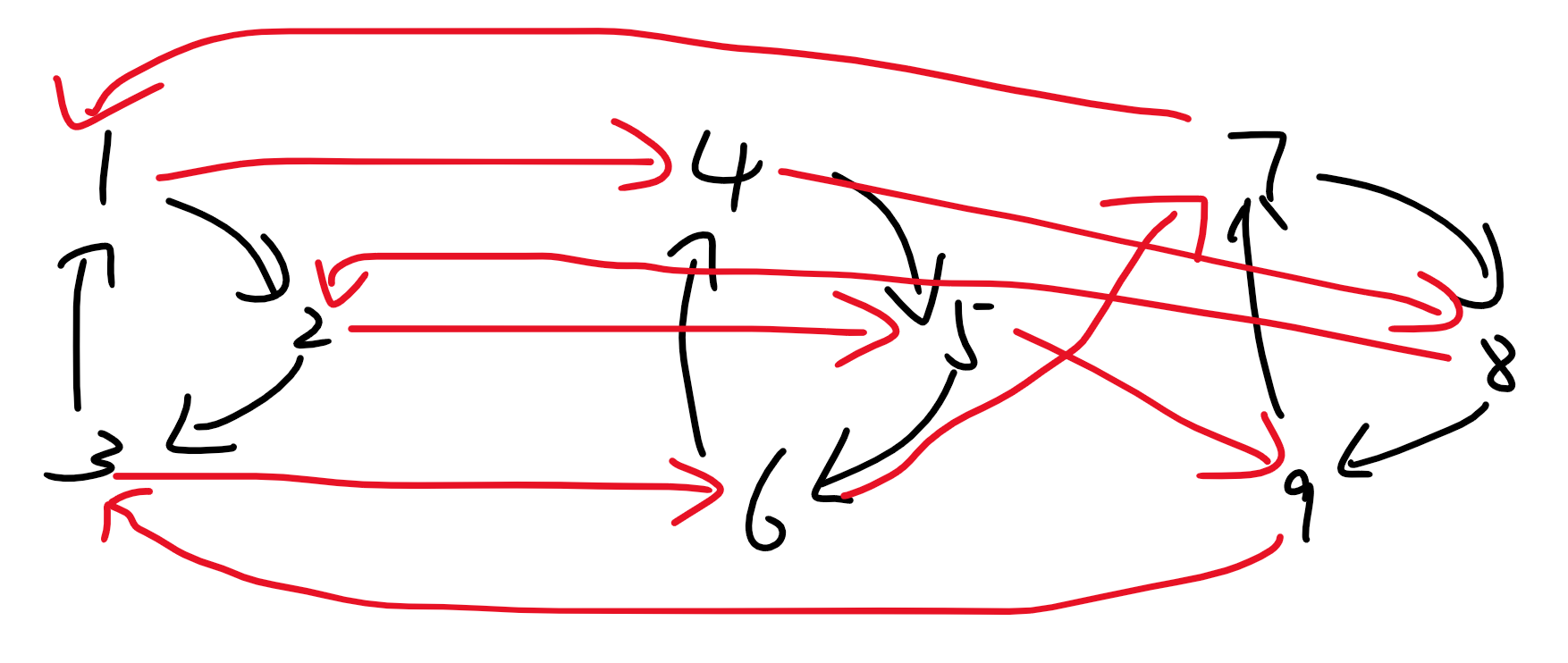
容易发现,对于前
个连通块来说,他们组成的大连通块长什么样子是无所谓的,所以方案数是 。
而对于后面的所有连通块,我们需要保证练成的样子与第一组同构,所以对于每一组的最后一个连通块,我们有唯一的连边限制。
也就是说,后面所有的方案数是 。
所以转移方程是 。
这样我们就可以在大约 的复杂度内完成转移。
dp 显然是正确的,但是他的复杂度太高了。而且似乎有些怪怪的?
似乎
这一维自始至终都是没有任何用处的?
考虑 中, 总共被乘了多少遍。
容易发现,上边的 表示
当前连通块个数 减去 连完一条边的连通块个数 加上 。
那么裂项相消之后不难想到:
结论:。
考虑归纳证明,对
显然成立。
假设对
的情况成立,那么对于
的情况:
显然是对的。
这样我们就可以在
的时间复杂度内完成这个 dp。
那么这个 dp 就可以只保留前两维,有转移式 。
总时间复杂度是 ,可以拿到 分。
时间复杂度瓶颈在于最后这个 dp。
dp 优化
考场上写完这里就只剩
分钟了,直接加了个文件走人了。
考虑先打表看看规律。
首先可以来看 ,可以发现有 。
证明的话还是归纳,显然对
都成立。
所以结论成立。
带回原来的式子。 有个阶乘,还有个指数,很烦,设 。
其中边界条件有一些变化,为 ,可以发现结果不变。
那么 。
而我们的目标是求出 。
考虑实际意义,
实际上是在说:
对于所有长度为 ,满足 ,且有 的序列 。
定义他的权值是 ,求所有合法序列的权值和。
考虑 的值是多少。
按照实际意义,我们枚举第
项填了哪个数字。
那么 。
这样我们就可以以一个类似快速幂的形式,求出所有 的值。
总时间复杂度是 。
写完力!
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
| #include<bits/stdc++.h>
using namespace std;
template<typename A>
using vc=vector<A>;
using ll=long long;
using pi=pair<int,int>;
using pl=pair<ll,ll>;
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
inline ll lread()
{
ll s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
const int mod=998244353;
int to[2001][2001];
ll C[2001][2001];
ll inv[2001];
ll jc[2001];
int fa[2001];
int fs[2001];
int n,m;
ll k;
struct node
{
ll f[2001];
ll g[2001];
node()
{
memset(f,0,sizeof(f));
memset(g,0,sizeof(g));
}
node operator * (node b)
{
node ans;
for(int u=1;u<=n;u++) for(int v=1;u*v<=n;v++)
ans.f[u*v]=(ans.f[u*v]+f[u]*b.g[u]%mod*b.f[v])%mod;
for(int u=1;u<=n;u++) ans.g[u]=g[u]*b.g[u]%mod;
return ans;
}
}dp[52],F;
inline int find(int num)
{
if(fa[num]==num) return num;
return fa[num]=find(fa[num]);
}
inline ll qow(ll a,ll b)
{
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
inline void init()
{
jc[0]=inv[0]=1;
for(int i=1;i<=n;i++)
{
jc[i]=jc[i-1]*i%mod;
inv[i]=qow(jc[i],mod-2);
}
for(int i=0;i<=n;i++)
{
C[i][0]=C[i][i]=1;
for(int j=1;j<i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
for(int i=1;i<=n;i++) dp[0].f[i]=1,dp[0].g[i]=i;
for(int i=1;(1ll<<i)<=k;i++) dp[i]=dp[i-1]*dp[i-1];
F=dp[0];
for(int i=0;(1ll<<i)<=k;i++) if((k-1)&(1ll<<i)) F=F*dp[i];
}
vc<int>nod[2001];
int siz[2001];
ll tp[2001];
inline ll get(int c,int s)
{
tp[0]=1;
for(int i=1;i<=c;i++)
{
tp[i]=0;
for(int j=1;j<=i;j++)
{
tp[i]=(tp[i]+tp[i-j]*C[i-1][j-1]%mod*F.f[j]%mod*jc[j-1]%mod*qow(s,j-1+k))%mod;
}
}
return tp[c];
}
pl h[2001];
const int mod1=998244853,mod2=1004535809;
const int B1=1145,B2=1919;
int a[3000001];
int id[2001];
int w[2001];
int cnt,len;
inline pl bfs(int s)
{
cnt=0,len=0;
for(int i=1;i<=n;i++) id[i]=0;
id[s]=++cnt,w[cnt]=s,a[++len]=id[s];
for(int i=1;i<=m;i++)
{
queue<int>que;
for(int j=1;j<=cnt;j++) que.push(w[j]);
while(!que.empty())
{
int u=que.front(),v=to[u][i];que.pop();
if(!id[v]) id[v]=++cnt,w[cnt]=v,que.push(v);
a[++len]=id[v];
}
}
ll ans1=0,ans2=0;
for(int i=1;i<=len;i++)
{
ans1=(ans1*B1+a[i])%mod1;
ans2=(ans2*B2+a[i])%mod2;
}
return pl(ans1,ans2);
}
int main()
{
read();n=read(),m=read(),k=lread();
init();
for(int i=1;i<=n;i++) fa[i]=i,fs[i]=1;
for(int i=1;i<=m*n;i++)
{
int u=read(),v=read();
to[u][read()]=v;
u=find(u),v=find(v);
if(u!=v) fa[u]=v,fs[v]+=fs[u];
}
for(int i=1;i<=n;i++) if(find(i)==i)
{
h[i]=bfs(i);
bool f=0;
for(int j=1;j<i;j++) if(nod[j].size()&&h[i]==h[j])
{
f=1;
nod[j].push_back(i);
break;
}
if(!f) nod[i].push_back(i),siz[i]=fs[i];
}
ll ans=1;
for(int i=1;i<=n;i++) if(nod[i].size()) ans=ans*get(nod[i].size(),siz[i])%mod;
printf("%lld\n",ans);
return 0;
}
|
感谢观看!



