场上推出了关键结论,写了一个
分做法。
但是不仅挂,而且假,气。
题目链接
题意
给定一棵 个点的树。
显然,共有
条端点不同的简单路径,令
为这些路径的一个子集。
现在有图 ,点集与这棵树相同。两个点 之间有边当且仅当存在路径 使得 覆盖点 。
集合 合法当且仅当 中任意两点距离不超过 。
求合法 数量,对 取模。
。
题解
首先这题有一个关键结论,并且可以很自然地被推出来,我在考场上的思路如下:
假设现在的点集
是合法的,那么对于根 ,他最多有一棵子树,使得其中有点不能一步到达
。
因为如果有两个点
都不能一步到达根,并且在两棵子树中,那么 到 至少需要 步,点集 就不合法了。
如果不存在这样的子树,那么所有点都能一步到达 ,否则只有一棵这样的子树,我们设子树的根为
。
显然,
子树外的点都可以一步到达 。
因为若 子树外有点 一步不能到达 ,则点 只能一步到达 ,而 又无法一步到达 子树内所有点,所以这样就会导致
不合法。
同时,与上面的讨论相同,对于点 ,他最多有一棵子树,使得其中有点不能一步到达
。
如果不存在这样的子树,那么所有点都能一步到达 ,否则只有一棵这样的子树,我们再设这棵子树的根为
。
以此类推。
最后我们会得到一个有限的序列 ,并且根据上述的推论,我们知道所有点都可以一步到达点
。
点集 合法的充要条件是 使得 可以一步到达所有点。
上面的证的是必要条件,充分条件就更好证了。
对于任意两个点 , 到 只需要一步, 到 只需要一步,那么 到 至多需要两步。
有了这个结论,我们就可以尝试计数了。
首先对于一个点集 ,不一定只存在一个上述的点 。
但是可以证明,所有的点
一定构成一个连通块,所以我们可以对于每一个点 ,计算他作为最高的点 有多少种方案。
那么我们需要计算的东西为:
对于每一个节点 ,计算所有点都可以一步到达 ,但存在点不能一步到达 的方数。
这样不好算,我们可以使用“点减边”容斥,转化为『所有点都能一步到达
的方案数』减去『所有点都能一步到达 与 的方案数』。
先考虑第一部分怎么做。
首先可以发现,只有所有叶子是“重要”的,因为所有叶子都与 有边,和所有点都与 右边等价。那么我们只需要看叶子与点
的边。
考虑容斥,设
表示已经考虑了 的前 棵子树(或子树外部分),当前已经钦定
个点不能与 连边的方案数。
设已经考虑过的部分有
个点,正在考虑的部分有
个叶子,
个非叶子,那么有转移:
暴力做总复杂度是
的,使用 NTT 可以优化到 或 。
我们发现,如果不考虑点
子树外的部分,那么总复杂度与树上背包相同,是 的。
假设 子树内有 个点,子树外有 个叶子与 个非叶子。那么有转移: 所以第一部分总复杂度是 的。
再来看第二部分。
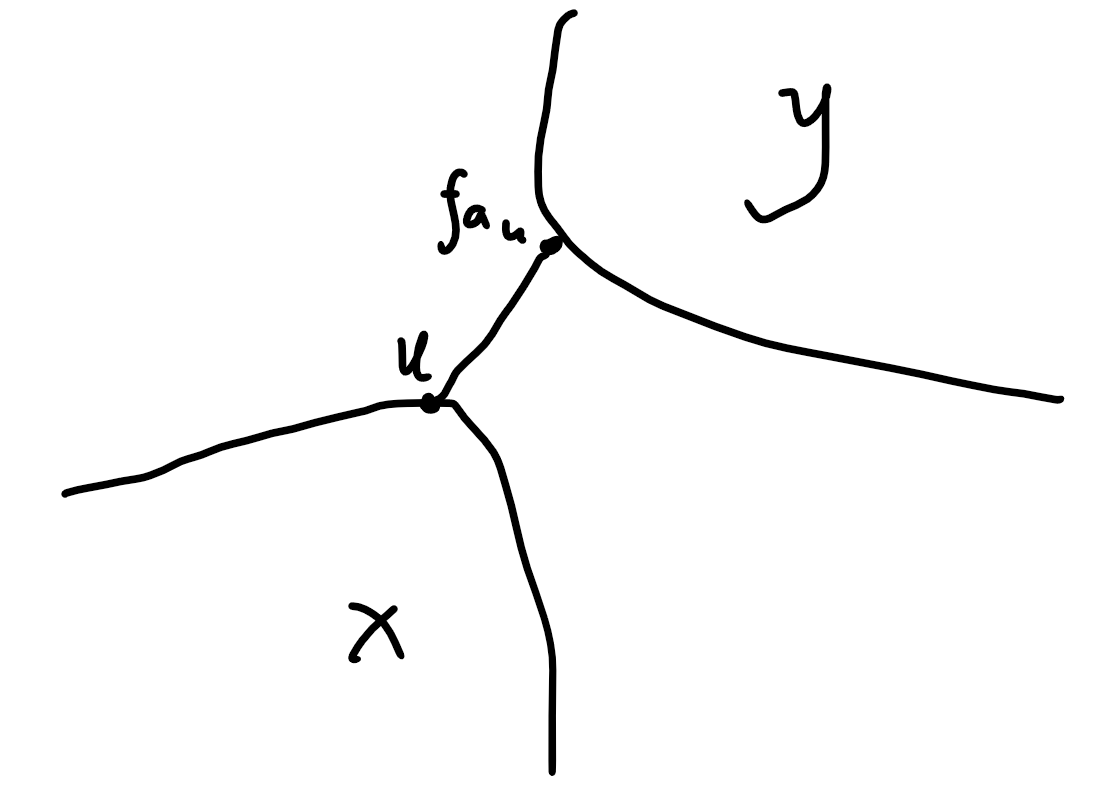
显然, 侧的叶子 需要一步可以到达 , 侧的叶子 需要一步可以到达 。
这就可以看成只有一棵子树的第一部分,我们手动做容斥,复杂度总和还是
。
这样我们就可以在
的复杂度内完成这道题。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
| #include<bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f3fll
#define debug(x) cerr<<#x<<"="<<x<<endl
using namespace std;
using ll=long long;
using ld=long double;
using pli=pair<ll,int>;
using pi=pair<int,int>;
template<typename A>
using vc=vector<A>;
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
const int mod=998244353;
template<const int N,const int M>
struct graph
{
int head[N+5];
int t[M+5];
int x[M+5];
int cntm;
graph(){ cntm=1;}
inline void clear(int n=N)
{
cntm=1;
for(int i=1;i<=n;i++) head[i]=0;
}
inline void ad(int u,int v)
{
cntm++;
t[cntm]=v;
x[cntm]=head[u];
head[u]=cntm;
}
inline void add(int u,int v)
{
ad(u,v);
ad(v,u);
}
inline int st(int num){ return head[num];}
inline int to(int num){ return t[num];}
inline int nx(int num){ return x[num];}
};
graph<3000,6000>g;
ll C[3001][3001];
ll h[3001][3001];
ll p[9000001];
ll dp[3001][3001];
int V[3001];
int fa[3001];
ll tp[3001];
int deg[3001];
int siz[3001];
int all;
ll ans;
int n;
inline void Add(ll &a,ll b)
{
(a+=b)%=mod;
}
inline void init()
{
for(int i=0;i<=n;i++)
{
C[i][0]=C[i][i]=1;
for(int j=1;j<n;j++) C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod;
}
p[0]=1;
for(int i=1;i<=n*n;i++) p[i]=p[i-1]*2%mod;
for(int i=0;i<=n;i++)
{
h[i][0]=1;ll val=p[i]-1;
for(int j=1;j<=n;j++) h[i][j]=h[i][j-1]*val%mod;
}
}
inline void merge(ll *dp,int n,int s1,int m,int s2)
{
for(int x=0;x<=n;x++) for(int y=0;y<=m;y++)
Add(tp[x+y],dp[x]*C[m][y]%mod*p[(s1-x)*(s2-y)+s2*(s2-1)/2]);
}
inline void run(int num)
{
int s1=0,l1=0;
for(int i=g.st(num);i;i=g.nx(i))
{
int p=g.to(i);
if(p!=fa[num]) s1+=siz[p],l1+=V[p];
}
int s2=n-2-s1,l2=all-l1-(deg[num]==1)-(deg[fa[num]]==1);
ll val=0;
for(int i=0;i<=l1;i++)
{
ll V=C[l1][i]*h[s1-i+1][l2]%mod*p[s2-l2+s1-i+(s2-l2)*(s1-i)]%mod;
if(i&1) val=(val+mod-V)%mod;
else val=(val+V)%mod;
}
val=val*p[n-1+(s1-1)*s1/2+(s2-1)*s2/2]%mod;
ans=(ans-val+mod)%mod;
}
void dfs(int num)
{
int v=(deg[num]==1);siz[num]=1,dp[num][0]=1;
for(int i=g.st(num);i;i=g.nx(i))
{
int p=g.to(i);
if(p==fa[num]) continue;
fa[p]=num;dfs(p);int val=V[p];
merge(dp[num],v,siz[num],val,siz[p]);
memcpy(dp[num],tp,sizeof(tp));
memset(tp,0,sizeof(tp));
siz[num]+=siz[p],v+=val;
}
ll val=0;int o1=all-v,o2=n-siz[num];
for(int i=0;i<=v;i++)
{
ll V=dp[num][i]*p[o2*(o2-1)/2+(siz[num]-i)*(o2-o1)]%mod*h[siz[num]-i][o1]%mod;
if(i&1) val=(val+mod-V)%mod;
else val=(val+V)%mod;
}
ans=(ans+val)%mod;
V[num]=v;
for(int i=g.st(num);i;i=g.nx(i))
{
int p=g.to(i);
if(p!=fa[num]) run(p);
}
return ;
}
int main()
{
n=read(),init();
if(n<=2){ printf("1\n");return 0;}
for(int i=1;i<n;i++)
{
int u=read(),v=read();
deg[u]++,deg[v]++;
g.add(u,v);
}
for(int i=1;i<=n;i++) if(deg[i]==1) all++;
dfs(1);
printf("%lld\n",ans);
return 0;
}
|
感谢观看!
