和蘑菇那题一样,也是莫名其妙就会了。不太确定是不是正解。
题目链接。
题意
现在有 个逻辑变量 。
定义一个条件 ,其中 且 ,称这个条件是成立的当且仅当有
。
定义一个字句为若干个条件,其中所有条件相关的变量互不相同,且相关变量的下标形成一个区间。
称一个字句是成立的当且仅当其中有至少一个条件是成立的。
定义合取范式为若干个字句,称一个合取范式是成立的当且仅当所有条件都是成立的。
给定一个合取范式,求有多少组变量的取值,使得这个合取范式是成立的。
。
所有字句的条件个数之和 。
题解
称一个条件
的所有变量下标形成的区间为 。
称一个区间 穿过一个位置
当且仅当有 且 。
设
为所有字句的条件个数,则本题中 。
首先来考虑一个 的
dp。
设 表示当前已经确定了前
个变量取值,满足如下条件的方案数:
- 所有 的字句 ,是成立的;
- 所有穿过位置
的子句且当前还未成立的字句中,
最靠左的一个为 ,不存在这样的字句时 ,存在多个这样的字句时选择编号最小的。
这里可能需要解释一下这个 dp 的定义,确定自己已经看懂的可以跳过。
首先是第一个条件,这个比较好理解,一个字句 对应的区间是 。
那么如果 ,就说明字句
牵扯到的所有变量的取值,都已经被确定下来了,这个时候我们显然可以直接说字句
是成立的/不成立的。
虽然 的字句
也已经能确定了此时是否成立,但是我的代码实现的是 ,这里就按 讲了。
然后是第二个条件。
根据定义,只要有一个条件成立,整个字句就成立,也就是说所有条件之间是或的关系。
若字句 穿过 ,且
之间的变量确定之后,已经有条件成立了,那么我们就可以直接说字句
成立了,因为后面无论怎么填他肯定都成立。
否则,字句 在
这个区间的所有条件都不满足,此时说字句 是目前还未成立的。
在所有目前还未成立的区间里面找到 最小的一个,这个字句就是 。
那么这里有一个问题,我们确定到
的时候,可能有很多区间当前未成立,为什么我们的状态里面只记录了一个 。
考虑,如果一个字句
当前未成立,那么
这一段所有的条件就都没有被满足,这个条件是相当严格的。
如果我们有两个字句
当且未成立,并且满足 ,那么我们明显可以知道,两个字句在
这一段的条件应该是完全一样的。
画个图方便理解:
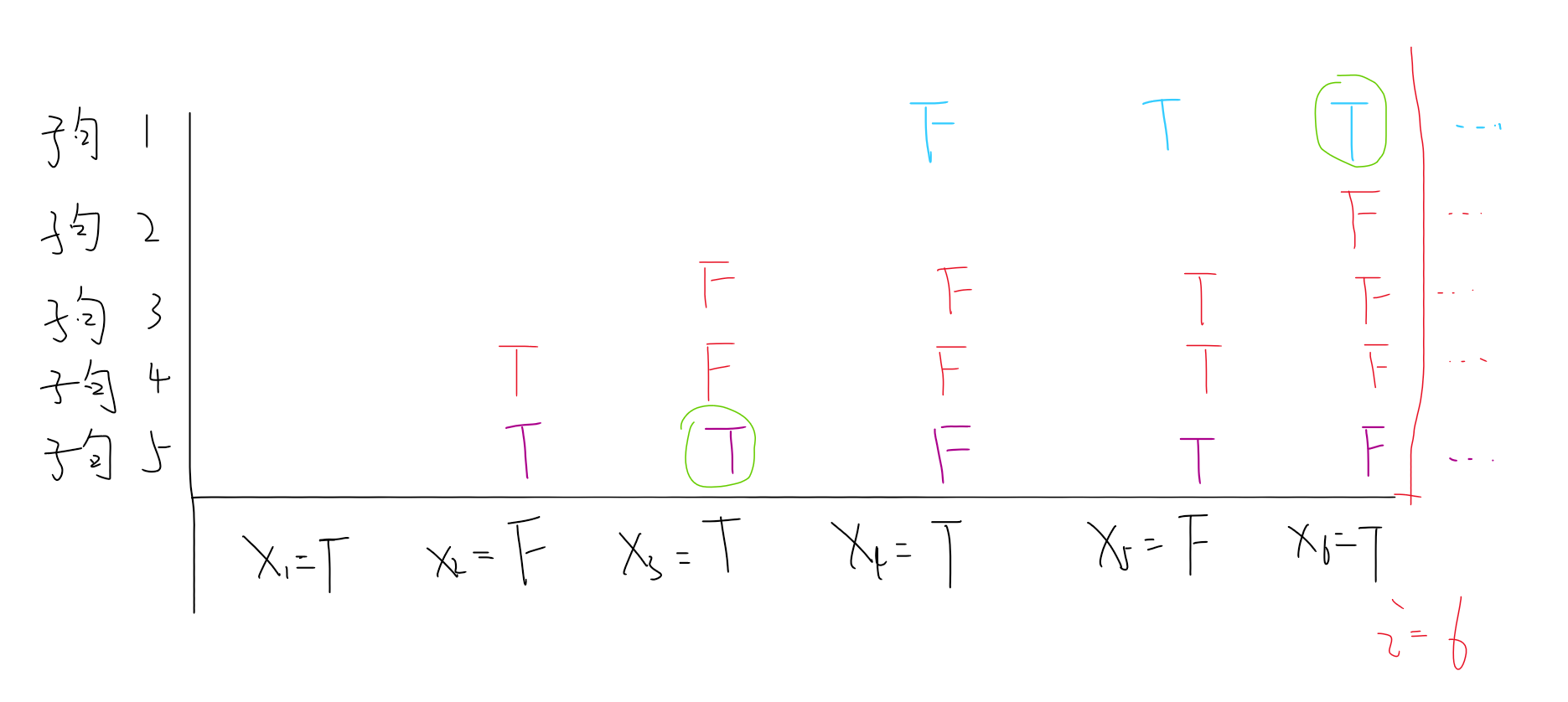
此处及以后,若说 是 的后缀,则表示在 之前的部分,字句 是字句 的后缀。
如图,字句 已经成立,字句
目前未成立。
那么显然 是 的一段后缀,且 都是 的一段后缀。
那么回到 dp 的状态,很容易说明,所有目前还未成立的字句 都是 的一段后缀。
那么显然,dp 的总状态是
的(因为状态中一定有 或 穿过 ),这是可以接受的。
问题在于如何进行转移,先来一点暴力的转移方式。
考虑
如何进行转移,首先如果有某个字句
满足 并且 是 的后缀,那么显然已经可以确定 不成立了,我们直接不转移 。
否则,我们枚举
的取值,重新找到满足条件的 ,并将 转移到 去。
最后的答案即为 。
这个做法直接写出来应该是 左右的,一些优化之后能做到
类似的复杂度。
容易发现,瓶颈在于如何快速找到 ,如果这个能解决这题就做完了。
那么考虑一下,能不能建出所有字句的字典树(只建出 之前的部分,字句 对应的字符串为其条件中 串起来)。
那么若 是 的后缀,则字典树上 是 的祖先(因为条件是倒着的,所以字典树上
是 的前缀,所以 是 的祖先)。
这样显然不太行,因为对于一个
来说,字典树大小就是
级别的,那么所有字典树总大小就是 级别的,这不可行。
那么考虑,我们能不能维护出字典树的虚树出来,虚树的总节点个数应当是
的,这听起来就很可行。
(其实说是虚树,其实不是平时说的那种虚树,但是差不多,看图吧)。
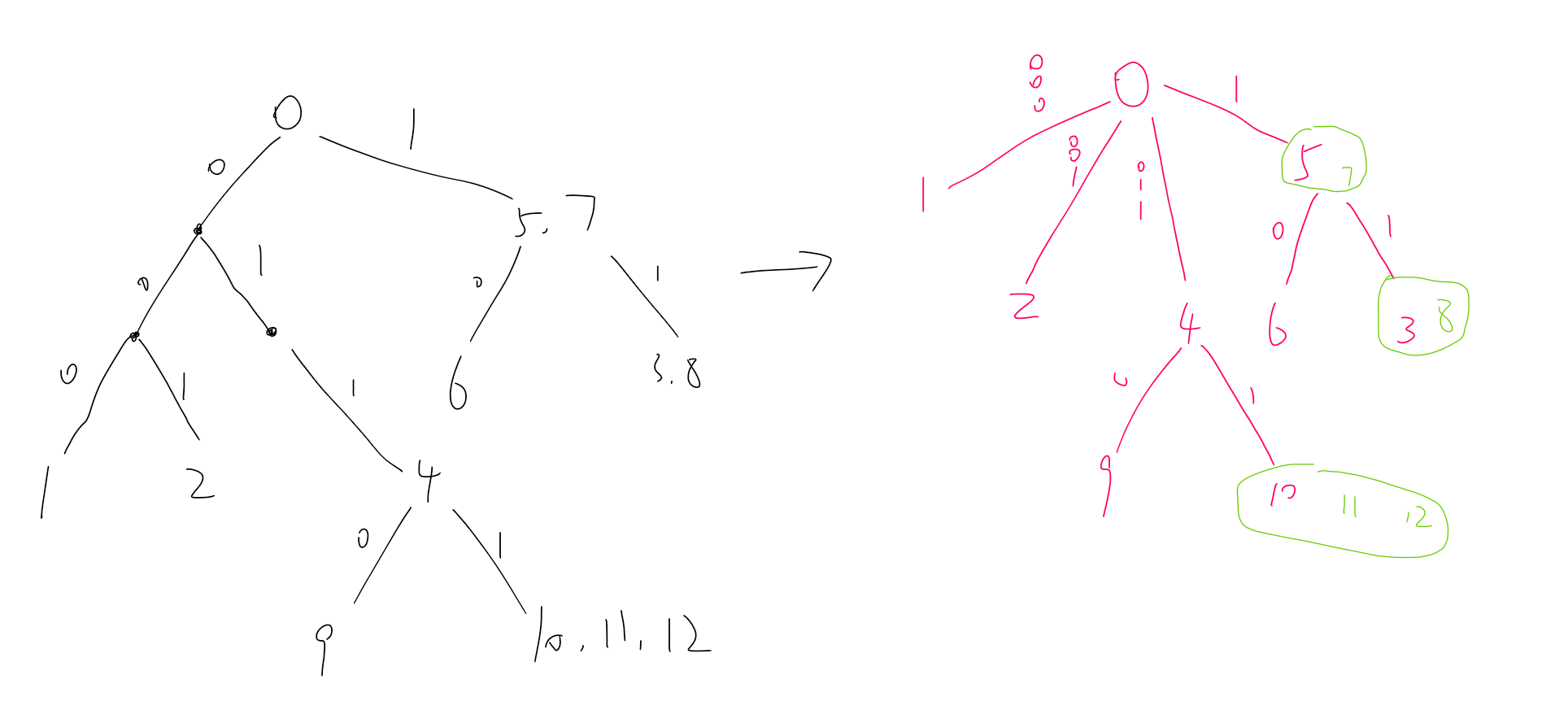 (显然每一条边所代表的字符串是不用维护的,但是为了方便理解我还是画上了)。
(显然每一条边所代表的字符串是不用维护的,但是为了方便理解我还是画上了)。
那么我们直接整个在这棵树上 dfs 一遍就能直接求出每一个点之后填 或者 会转移到哪个点。
所有 dfs 的复杂度之和应当与总结点个数相等,也就是 的。
那么问题在于如何维护这棵树,这也是相当简单的!
考虑将 往后扩展一位变成 的时候整棵树会如何变化。
首先, 的字句 会从这棵树上消失(此部分包括节点 ),剩余的所有字句共有两种,分别是 这个位置是 的。
而新加入的
这一位,应当会添加在字典树的最上方。
那么就直接把两种字句分开维护出新的虚树,然后再最上面连到一起就好了。
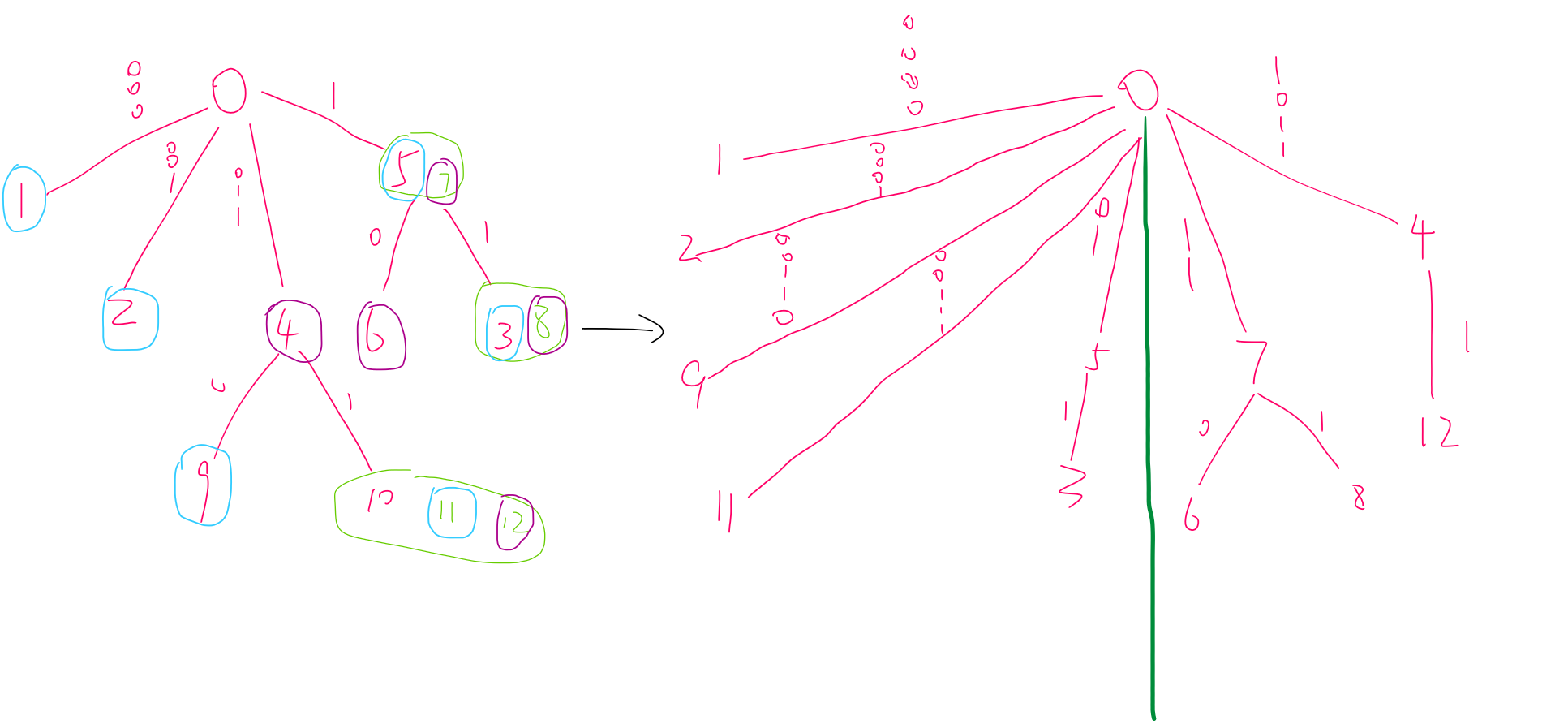
左边被蓝色圈出的是下一位为 的字句,紫色圈出的是下一位为
的字句,没有圈出的是
或满足 的字句。
这个维护过程也比较简单,dfs
一遍之后就可以算出每一个点的父亲节点,和上面一块 dfs 就行。
时间复杂度是 。
代码
我的 dp 值直接用 map 存的,所以会多一个 ,最后一个点几乎卡着过的。
如果你被卡了,可以考虑直接开数组,然后开一个桶记一下每一个点 dp
值存在桶里哪个位置,这样就线性了。
注意字句的个数并不是 ,而是不确定的,需要你根据读入自己确定。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
| #include<bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f3fll
#define debug(x) cerr<<#x<<"="<<x<<endl
using namespace std;
using ll=long long;
using ld=long double;
using pli=pair<ll,int>;
using pi=pair<int,int>;
template<typename A>
using vc=vector<A>;
template<typename A,const int N>
using aya=array<A,N>;
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
inline int read(char &ch)
{
int s=0,w=1;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
const int mod=1000000007;
int fa[1000005],fap[1000005];
vc<int>son[1000005];
vc<int>bel[1000005];
map<int,ll>dp[1000005];
vc<int>l[1000005];
vc<int>a[1000005];
vc<int>node;
int n;
inline int get(int x,int y)
{
return a[x][y-abs(a[x][0])];
}
void dfs(int num,int f0,int f1,int i,bool f)
{
vc<int>nod0,nod1;int rt0=0,rt1=0;
for(int p:bel[num]) if(abs(a[p].back())>=i)
{
if(get(p,i)>0) nod1.push_back(p);
else nod0.push_back(p);
}
else f=1;
vc<int>mem=son[num];
bel[num].clear();son[num].clear();
if(nod0.size()) rt0=nod0[0],bel[rt0]=nod0,son[f0].push_back(rt0),f0=rt0;
if(nod1.size()) rt1=nod1[0],bel[rt1]=nod1,son[f1].push_back(rt1),f1=rt1;
if(!f)
{
if(rt0) fa[rt0]=f1,node.push_back(rt0),fap[rt0]=rt0;
if(rt1) fa[rt1]=f0,node.push_back(rt1),fap[rt1]=rt1;
}
if(!num) fa[0]=f0,fap[0]=f1;
for(int p:mem) dfs(p,f0,f1,i,f);
}
inline void output(int p)
{
printf("output %d fa=%d,%d:\n",p,fa[p],fap[p]);
for(int i:bel[p]) printf("%d ",i);;putchar('\n');
for(int i:son[p]) printf("%d ",i);;putchar('\n');
for(int i:son[p]) output(i);
}
int main()
{
n=read();a[0].push_back(0);int m=0;
while(1)
{
char ch;
while(((ch=getchar())!='(')&&(ch!=EOF));
if(ch!='(') break;
m++;
while(true)
{
ch=getchar();bool f=0;
if(ch=='~') f=1,ch=getchar();
int v=read(ch);if(f) v=-v;
a[m].push_back(v);
if(ch==')') break;
getchar(),getchar();
}
sort(a[m].begin(),a[m].end(),[](int x,int y){ return abs(x)<abs(y);});
l[abs(a[m][0])].push_back(m);
}
dp[0][0]=1;
for(int i=1;i<=n;i++)
{
bel[0]=l[i];
sort(bel[0].begin(),bel[0].end());
node.clear();dfs(0,0,0,i,false);
node.push_back(0);
for(int p:node) if(dp[i-1].count(p))
{
(dp[i][ fa[p]]+=dp[i-1][p])%=mod;
(dp[i][fap[p]]+=dp[i-1][p])%=mod;
}
}
printf("%lld\n",dp[n][0]);
return 0;
}
|
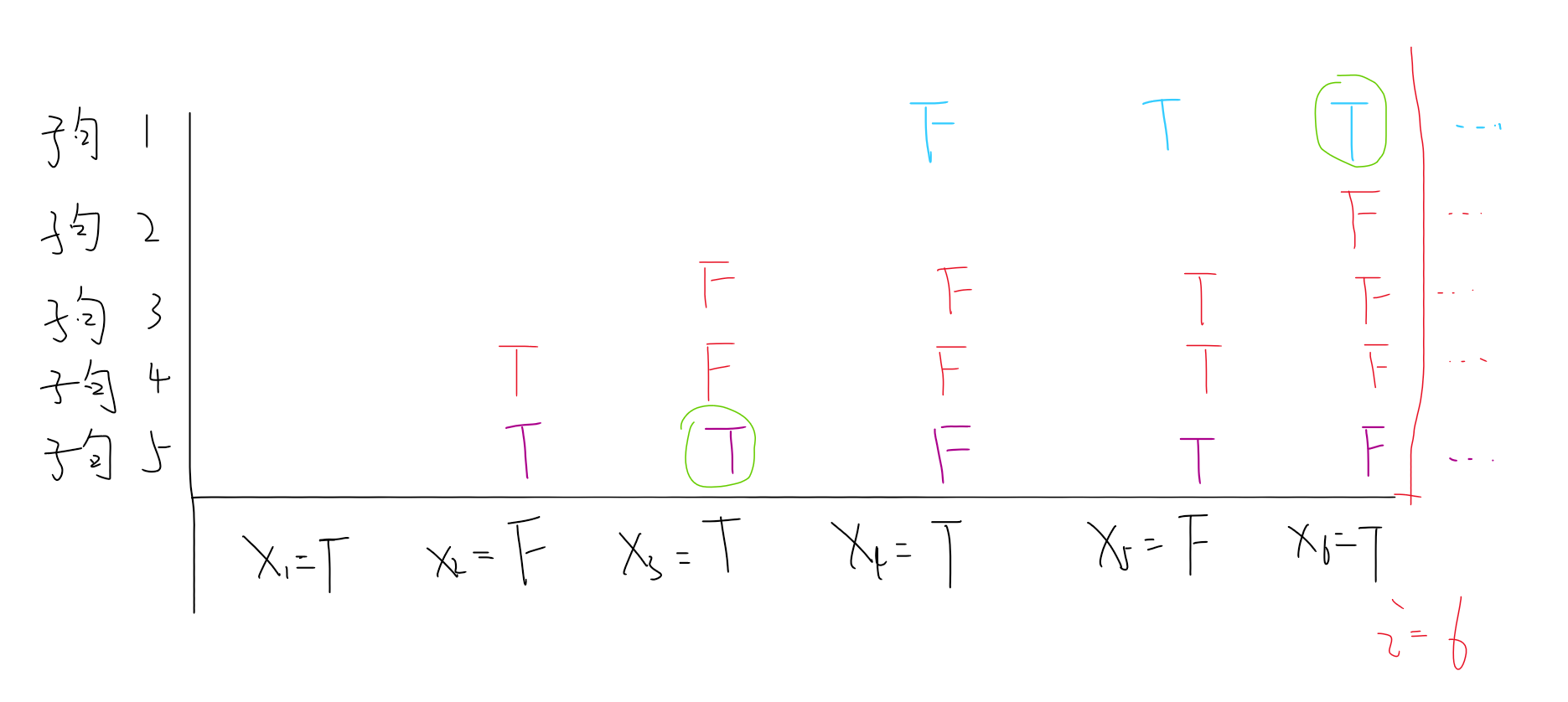
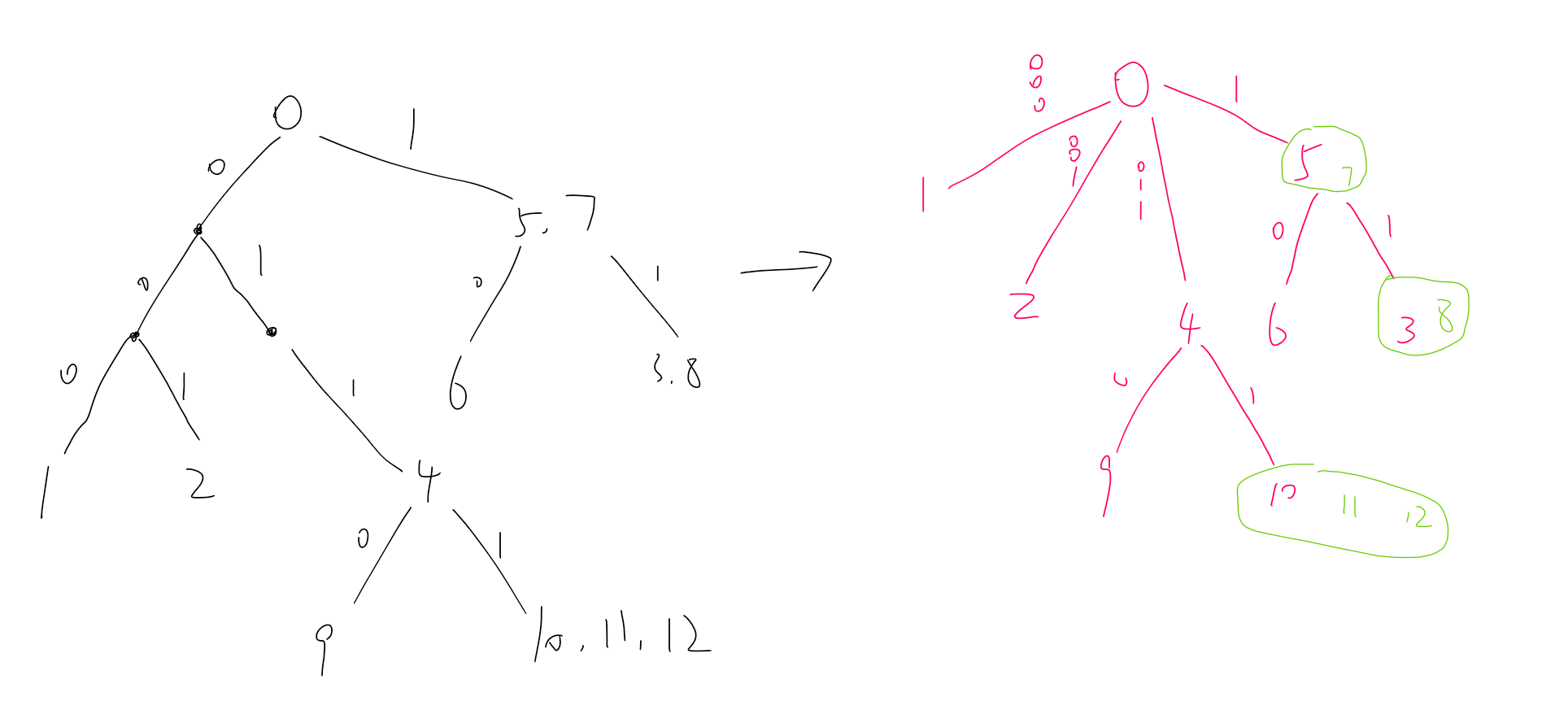 (显然每一条边所代表的字符串是不用维护的,但是为了方便理解我还是画上了)。
(显然每一条边所代表的字符串是不用维护的,但是为了方便理解我还是画上了)。