打模拟赛遇到的,同学都是一眼秒,只有我在乱七八糟贪。
最近已经遇到好几个题是一眼dp,但我没看出来了。
题目链接
题意
现在有
个人在一个队列里面,每一个人有一个能力值是 ,保证 是奇数。
每一次取出队列中最前面的三个人,去掉能力最大的和最小的,把剩下的那个人(中位数)放到队尾。
最后剩下一个人的时候,留下的那个人就是这种排队方案的权值。
现在已经有
个人确定了自己初始时在队列中的位置,你需要给剩下的 个人排好位置,使得权值最大。
题解
首先我们看到中位数,就能很明显想到二分。
所以我们二分,现在问题变成了:每个人能力值为 或 ,能否使最后的权值是 。
这个问题似乎不太好做,我们来模拟一下,假如当前队列中人的编号为 ,我们来模拟这个过程。
初始时,队列为:。
首先拿出前三个人,并将中位数插入队尾。我们并不知道哪个人是中位数。
所以我们可以稍微转化一下操作,把他变成这个样子:
把队列的前三个人一起拿走,并且加入一个新人,能力值为前三个人的中位数。
所以我们现在假设加入的人是
号。
队列为:。
依次执行这个过程,得到:
所以我们的问题就是
号人能力是否能为 。
通过这个模拟的过程,我们完全可以知道每一个人的能力值是由哪三个人决定的,我们把图画出来。
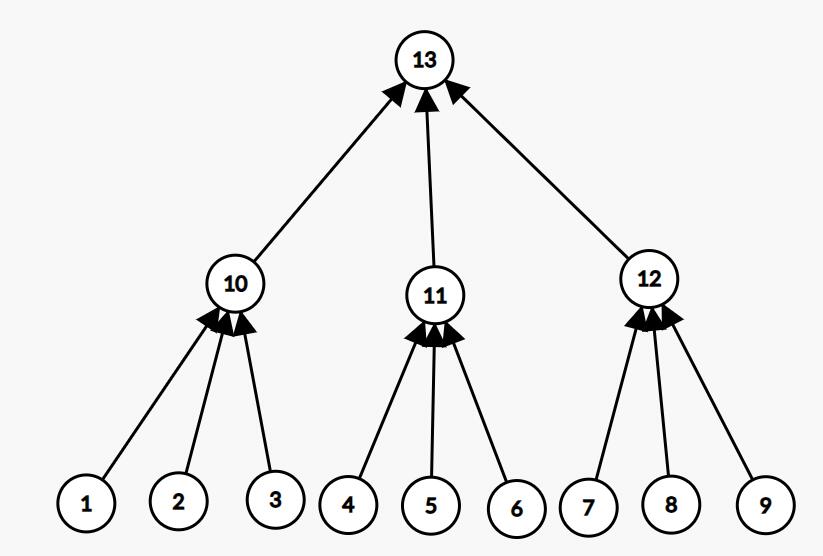
我们发现,这种关系一定会是一个树状的结构。
同时,我们考虑到权值只有 和
,发现实际就是在问,能否合理地分配
的位置,使得根的权值为 。
那么我们考虑对其进行树形dp。
设 表示,如果要让 的权值为 ,至少需要在子树内额外放置多少个 。
当 为叶节点,且上面已经有一个
时,不需要多余填,这里的值就是
,所以 ;
当 为叶节点,且上面已经有一个
时,这个位置不可能是 ,那么 ;
当
为叶节点,且上面时还没有填数字时,;
否则假设 的三个儿子为 ,那么 。
假如我们有 个 暂未放置,那么在 时有解。
代码
实际上在写的时候,不需要建树。
直接使用队列进行模拟即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| #include<bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f3fll
using namespace std;
using ll=long long;
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
ll dp[200001];
int a[100001];
int b[100001];
int c0,c1;
int n,m;
inline bool cal(int num)
{
c0=c1=0;
for(int i=1;i<=n-m;i++)
{
if(b[i]>=num) c1++;
else c0++;
}
queue<int>que;int cnt=0;
for(int i=1;i<=n;i++)
{
++cnt;
if(a[i]==-1) dp[cnt]=1,que.push(cnt);
else if(a[i]>=num) dp[cnt]=0,que.push(cnt);
else dp[cnt]=0x3f3f3f3f,que.push(cnt);
}
while(que.size()>1)
{
int a1=que.front();que.pop();
int a2=que.front();que.pop();
int a3=que.front();que.pop();
cnt++,dp[cnt]=dp[a1]+dp[a2]+dp[a3]-max(dp[a1],max(dp[a2],dp[a3]));
que.push(cnt);
}
return dp[que.front()]<=c1;
}
int main()
{
n=read(),m=read();
memset(a,-1,sizeof(a));
for(int i=1;i<=m;i++)
{
int x=read(),y=read();
a[y]=x;
}
for(int i=1;i<=n-m;i++) b[i]=read();
int ans=0;
for(int i=1<<30;i;i>>=1) if(cal(ans+i)) ans+=i;
printf("%d\n",ans);
return 0;
}
|
感谢观看!
