FFT学习笔记

FFT 的中文名称为快速傅里叶变换，英文全称为 Fast Fourier Transform。

主要用于快速计算多项式乘法。

系数表示法

我们知道，每一个多项式都有唯一的一组系数，每一组系数也对应着唯一的一个多项式，所以我们可以用一组系数来表示一个多项式：

点值表示法

我们可以把这个多项式看作平面直角坐标系上的一个函数，那么我们就可以从上面选个点，这些点一定可以唯一表示这个多项式。

为什么这么说呢？我们假设这个点分别是。

那么我们可以由此列出方程：我们将这些和带入方程组中，便得到了一个有个方程和个未知数的方程组。只要所给出的互不相同，那么我们正好可以解得唯一的一组，也就可以表示这个多项式了。

FFT的基本理论

FFT 在 OI 中干的事情就是快速求出两个多项式的乘积，下面我们来看他是怎么做到的。

首先，我们还是把与由系数表示法变为点值表示法，这个过程被叫为 DFT。

假设函数对应的点坐标分别为，函数对应的点坐标分别为。（没错，他们的横坐标要相等）

那么我们就可以得到。

那么现在我们知道了的点值表示法，现在我们就可以将他表示为系数表示法，这个过程被叫为 IDFT。

FFT 的理论就是这个样子，但是我们也知道 DFT 暴力的时间复杂度为，IDFT 采用高斯消元的做法时间复杂度也为，使用拉格朗日插值可以做到。显然，FFT 的效率还不如暴力高。那么我们的主要问题就为优化 FFT 了。

当然，上述做法有一些漏洞。假如与的最高次项系数都为，那么的最高次项系数就是。此时肯定是无法用个点表达这个多项式了，所以实际上我们需要不止个点参与计算。

坐标的取值

我们会发现无论如何，似乎 FFT 的时间复杂度都无法得到有效的优化，那么如果我们取的横坐标是一些特殊的值呢？

复数

我们知道，方程的解在实数域下只有个，即或，但是这个方程在复数域下却有个解。

设，那么这个方程的解便为。

另一方面我们可以根据欧拉公式，也可以得到。

放一张 oi-wiki 上的图片，有助于理解。

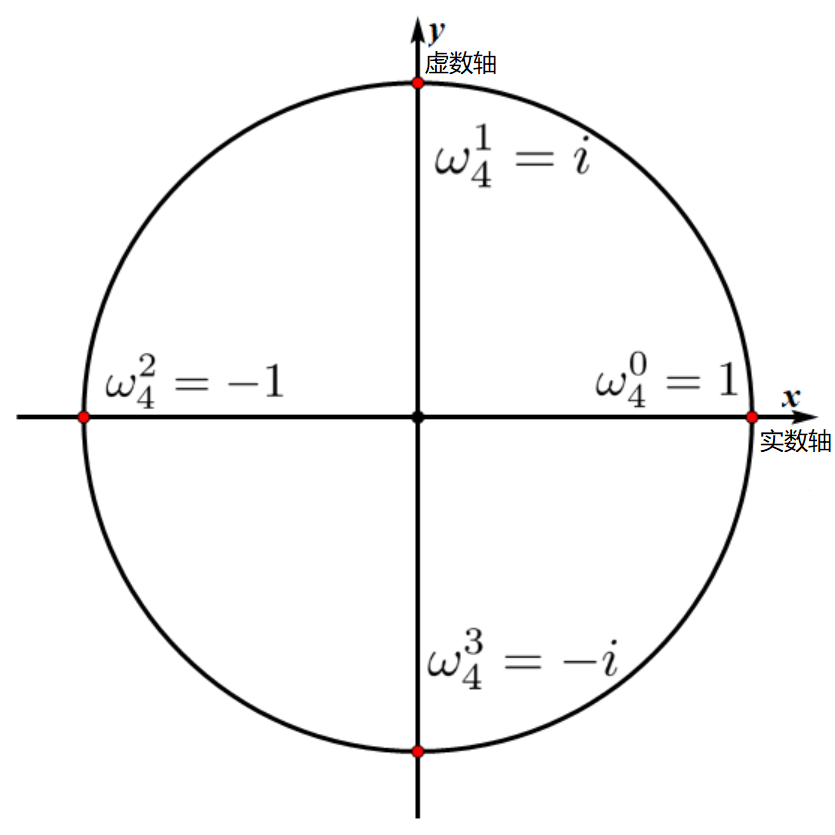
复数的性质

对于任意的正整数及整数，有：

三个公式放到上面那张图里面都不难理解。

复数的运算

设，下面我们来推导复数的计算。复数的除法也是可以推导的，不过我们暂时用不到。

我们可以打出一份复数的结构体。

代码

struct fs//因为英语不好，所以就用拼音了......
{
    double x,y;//x为实部，y为虚部，也就是说这个复数为x+yi
    fs(double xx=0,double yy=0){ x=xx,y=yy;}
    fs operator + (fs b){ return fs(x+b.x,y+b.y);}
    fs operator - (fs b){ return fs(x-b.x,y-b.y);}
    fs operator * (fs b){ return fs(x*b.x-y*b.y,x*b.y+y*b.x);}
};

DFT

首先我们要将一个函数由系数表示法变为点值表示法，我们设这个函数为，且第项的系数为。

为了方便起见，我们设的项数为的整数次幂，如果项数不够可以补齐。

首先我们设： $为偶数且为奇数且$

那么就会有。

我们现在要得到个点的坐标，他们的横坐标分别为，下面我们来推式子~~（颓柿子）~~。 $这里运用了公式（）这里运用了公式（）这里运用了公式（）$ 可以发现什么？与经过化简后第一项相同，第二项互为相反数。这时我们是否可以快速进行 DFT 呢？

设对一个项数为的多项式进行 DFT 的过程时间复杂度为。

根据主定理分析可得时间复杂度为。

那么我们就可以把 DFT 的代码打出来。

代码

//这里前面还需要复数的结构体，但是前面已经打过了，不再重复
const double PI=acos(-1);//这个函数可以得到精确的圆周率
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
void DFT(fs *a,int n)
{
    if(n==1) return ;
    vector<fs>mem(n);//开一个数组记录之前的值
    for(int i=0;i<n;i++) mem[i]=a[i];
    for(int i=0;i<n/2;i++) a[i]=mem[2*i];
    for(int i=0;i<n/2;i++) a[i+n/2]=mem[2*i+1];
    //将一个函数f进行分治，a的前半部分为g，后半部分为h
    DFT(a,n/2),DFT(a+n/2,n/2);//进行分治
    fs now(1,0),step=omega(n);
    for(int i=0;i<n/2;i++)
    {
        //根据公式计算a[i]与a[i+n/2]
        //注意这里顺序不能错，一定要先计算a[i+n/2]
        fs num=a[i+n/2];
        a[i+n/2]=a[i]-now*num;
        a[i]=a[i]+now*num;
        now=now*step;
    }
}

这个代码还可以进行一些常数优化，不过我们后面一起进行优化。

IDFT

这个时候我们得到了答案多项式的点值表示法，我们设这个函数的第项的系数为，个点的坐标分别为。

首先我们可以换一个方式表示这些点与系数的关系。我们把这些式子写成矩阵的形式。我们再来看一看最左边的这个矩阵有什么性质：右边的那个矩阵恰好是单位矩阵的倍，那么我们就可以把最上面的那个矩阵进行转化。我们有什么好方法？照样采用 DFT 的方法，对函数按照奇偶进行计算。

首先我们知道，那么我们再对上面的式子进行转化。令

还是像上面一样，我们设： $为偶数且为奇数且$ 那么就有：我们又可以发现什么？与经过化简后第一项相同，第二项互为相反数。这时我们是否可以快速进行 IDFT 呢？

设对一个项数为的多项式进行 IDFT 的过程时间复杂度为。

分析可得时间复杂度为。

那么我们就可以把 IDFT 的代码打出来。

代码

//这里前面还需要复数的结构体，但是前面已经打过了，不再重复
const double PI=acos(-1);//这个函数可以得到精确的圆周率
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
void IDFT(fs *a,int n)
{
    if(n==1) return ;
    vector<fs>mem(n);//开一个数组记录之前的值
    for(int i=0;i<n;i++) mem[i]=a[i];
    for(int i=0;i<n/2;i++) a[i]=mem[2*i];
    for(int i=0;i<n/2;i++) a[i+n/2]=mem[2*i+1];
    //将一个函数f进行分治，a的前半部分为g，后半部分为h
    IDFT(a,n/2),IDFT(a+n/2,n/2);//进行分治
    fs now(1,0),step=omega(n);
    step.y=-step.y;
    for(int i=0;i<n/2;i++)
    {
        //根据公式计算a[i]与a[i+n/2]
        //注意这里顺序不能错，一定要先计算a[i+n/2]
        fs num=a[i+n/2];
        a[i+n/2]=a[i]-now*num;
        a[i]=a[i]+now*num;
        now=now*step;
    }
}
//别忘了最后要把所有a[i]变为a[i]/n

~~没错这一整段是从上面那里复制之后改了一下。~~

FFT的优化

首先解决一个问题：我们在进行 DFT 与 IDFT 时都默认为一个形如的数字，但是我们在实际应用中并不会全是这种情况。

其实只需要取一个比这个数大并且的最小的就可以了。

合二为一

我们可以发现 DFT 与 IDFT 的函数中只有一句不一样，那么我们就可以把这两个函数合二为一。

现在我们已经打得差不多了，我们来提交试一下。

代码：

代码

#include<cstdio>
#include<vector>
#include<cmath>
using namespace std;
const double PI=acos(-1);//这个函数可以得到精确的圆周率
struct fs//因为英语不好，所以就用拼音了......
{
    double x,y;//x为实部，y为虚部，也就是说这个复数为x+yi
    fs(double xx=0,double yy=0){ x=xx,y=yy;}
    fs operator + (fs b){ return fs(x+b.x,y+b.y);}
    fs operator - (fs b){ return fs(x-b.x,y-b.y);}
    fs operator * (fs b){ return fs(x*b.x-y*b.y,x*b.y+y*b.x);}
};
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
fs a[5000000];
fs b[5000000];
void DFT(fs *a,int n,bool dft)
{
    //当dft为1的时候，进行DFT
    //当dft为0的时候，进行IDFT
    if(n==1) return ;
    vector<fs>mem(n);//开一个数组记录之前的值
    for(int i=0;i<n;i++) mem[i]=a[i];
    for(int i=0;i<n/2;i++) a[i]=mem[2*i];
    for(int i=0;i<n/2;i++) a[i+n/2]=mem[2*i+1];
    //将一个函数f进行分治，a的前半部分为g，后半部分为h
    DFT(a,n/2,dft),DFT(a+n/2,n/2,dft);//进行分治
    fs now(1,0),step=omega(n);
    if(!dft) step.y=-step.y;
    for(int i=0;i<n/2;i++)
    {
        //根据公式计算a[i]与a[i+n/2]
        //注意这里顺序不能错，一定要先计算a[i+n/2]
        fs num=a[i+n/2];
        a[i+n/2]=a[i]-now*num;
        a[i]=a[i]+now*num;
        now=now*step;
    }
}
int n,m;
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
    for(int i=0;i<=m;i++) scanf("%lf",&b[i].x);
    m+=n,n=1;for(;n<=m;n<<=1);
    DFT(a,n,1),DFT(b,n,1);
    for(int i=0;i<n;i++) a[i]=a[i]*b[i];
    DFT(a,n,0);
    for(int i=0;i<=m;i++) printf("%d ",(int)(a[i].x/n+0.5));
    return 0;
}

提交记录

蝴蝶变换

虽然这份代码 AC 了，但是它显然还不够快，我们还需要进行亿点点常数优化。

可以注意到一个过程中常数比较大的地方：就是 DFT 过程中数组的打乱。不难发现，这个部分的时间复杂度为，而且我们这里还多开了大约个复数（就是那个叫 mem 的 vector）。

我们来找一下这个地方数字变化的规律，这里以举例，而且数字的下标以二进制书写，便于发现规律。 $初始：第一次变换：第二次变换：第三次变换：$

我们可以发现什么？

没错，交换前后每个位置上的数字的二进制位全部是相反的。

当然这是我们发现的结论，现在我们来证明。

采用数学归纳法：

首先我们知道当时，这个结论显然成立，因为这个时候只有一个数字。

现在我们要证明当时结论成立，我们假设当时结论成立。

设为第个位置上的数在时经过交换之后到的地方，一个数字二进制下的最低位为。

那么。

显然，的最后一位放到了最前面，前面的位经过翻转后放到了后面，这个结论显然是正确的。

现在要做的就是快速计算这个翻转后的值，显然也是可以快速进行计算的。

代码

//wh[i]表示i这个数经过翻转以后所对应的值
//wh[0]=0,不进行计算
for(int i=1;i<n;i++) wh[i]=(wh[i>>1]>>1)+((i&1)?n>>1:0);
//当i的最后一位为0时，wh[i]=(wh[i>>1]>>1)
//当i的最后一位为1时，wh[i]=(wh[i>>1]>>1)+(n>>1)
//这个显然是正确的，道理和上面证明的过程差不多。

这部分时间复杂度为，这种 FFT 比起之前的常数小了一些。

此外还有一些别的优化，例如提前计算 step 的值，将递归改为循环等，由于比较简单，这里不详细展开。

我们就直接重写代码，看一下提交结果。

代码：

代码

#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
const double PI=acos(-1);
struct fs
{
    double x,y;
    fs(double xx=0,double yy=0){ x=xx,y=yy;}
    fs operator + (fs b){ return fs(x+b.x,y+b.y);}
    fs operator - (fs b){ return fs(x-b.x,y-b.y);}
    fs operator * (fs b){ return fs(x*b.x-y*b.y,x*b.y+y*b.x);}
};
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
fs step[5000001];
int wh[5000001];
fs a[5000000];
fs b[5000000];
int n,m;
void DFT(fs *a,int n,bool dft)
{
    for(int i=0;i<n;i++) if(i<wh[i]) swap(a[i],a[wh[i]]);
    //有这个if就可以确保只换一次，当然也可以写成if(i>wh[i])...
    for(int len=2;len<=n;len<<=1)
    {
        fs ste=step[len];
        if(!dft) ste.y=-ste.y;
        for(int l=0;l<n;l+=len)
        {
            fs now(1,0);
            for(int i=l;i<l+len/2;i++)
            {
                fs num=a[i+len/2]*now;
                a[i+len/2]=a[i]-num;
                a[i]=a[i]+num;
                now=now*ste;
            }
        }
    }
}
void FFT(fs *a,fs *b,int n)
{
    for(int i=2;i<=n;i<<=1) step[i]=omega(i);
    for(int i=1;i<n;i++) wh[i]=(wh[i>>1]>>1)+((i&1)?n>>1:0);
    DFT(a,n,1),DFT(b,n,1);
    for(int i=0;i<n;i++) a[i]=a[i]*b[i];
    DFT(a,n,0);
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
    for(int i=0;i<=m;i++) scanf("%lf",&b[i].x);
    m+=n,n=1;for(;n<=m;n<<=1);
    FFT(a,b,n);
    for(int i=0;i<=m;i++) printf("%d ",(int)(a[i].x/n+0.5));
    return 0;
}

提交记录

三次变两次

三次变两次是通过一种特殊的方法，少进行一次 DFT 的优化（由原来的次 DFT 和 IDFT变为各有一次）。

假设我们现在想要求两个多项式和的乘积，不妨设复多项式 。

那么就有。

它的虚部不就正好是我们要求的乘积的两倍吗？

代码：

代码

#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
const double PI=acos(-1);
struct fs
{
    double x,y;
    fs(double xx=0,double yy=0){ x=xx,y=yy;}
    fs operator + (fs b){ return fs(x+b.x,y+b.y);}
    fs operator - (fs b){ return fs(x-b.x,y-b.y);}
    fs operator * (fs b){ return fs(x*b.x-y*b.y,x*b.y+y*b.x);}
};
fs omega(int n){ return fs(cos(2*PI/n),sin(2*PI/n));}
fs step[5000001];
int wh[5000001];
fs a[5000000];
int n,m;
void DFT(fs *a,int n,bool dft)
{
    for(int i=0;i<n;i++) if(i<wh[i]) swap(a[i],a[wh[i]]);
    //有这个if就可以确保只换一次，当然也可以写成if(i>wh[i])...
    for(int len=2;len<=n;len<<=1)
    {
        fs ste=step[len];
        if(!dft) ste.y=-ste.y;
        for(int l=0;l<n;l+=len)
        {
            fs now(1,0);
            for(int i=l;i<l+len/2;i++)
            {
                fs num=a[i+len/2]*now;
                a[i+len/2]=a[i]-num;
                a[i]=a[i]+num;
                now=now*ste;
            }
        }
    }
}
void FFT(fs *a,int n)
{
    for(int i=2;i<=n;i<<=1) step[i]=omega(i);
    for(int i=1;i<n;i++) wh[i]=(wh[i>>1]>>1)+((i&1)?n>>1:0);
    DFT(a,n,1);
    for(int i=0;i<n;i++) a[i]=a[i]*a[i];
    DFT(a,n,0);
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
    for(int i=0;i<=m;i++) scanf("%lf",&a[i].y);
    m+=n,n=1;for(;n<=m;n<<=1);
    FFT(a,n);
    for(int i=0;i<=m;i++) printf("%d ",(int)(a[i].y/n/2+0.5));
    return 0;
}

提交记录

可以看到，快了不少。