思维题,但是我没有思维,所以我不会
看完题解之后感觉这道题其实是很可做的,推导过程也很顺畅
题目链接
题意
现在有两条河岸,分别坐落着
座城市,对于同一条河岸的两座城市 都有一条有向边 。
现在还有 条额外边,第 条边连接了上河岸第 座城市与下河岸第 座城市,这些额外边都还没有定向。
为每一条额外边指定一个方向,使得强连通分量个数最少
输出最少的个数,并构造方案。
题解
COCI 的题总是给我一种去了就要爆零的感觉。
本题的难点显然在于构造方案,因为方案出来了,只需要一个 tarjan
就可以求出第一问的答案。
来想一想,对于每一条边来说,怎样连会产生贡献?
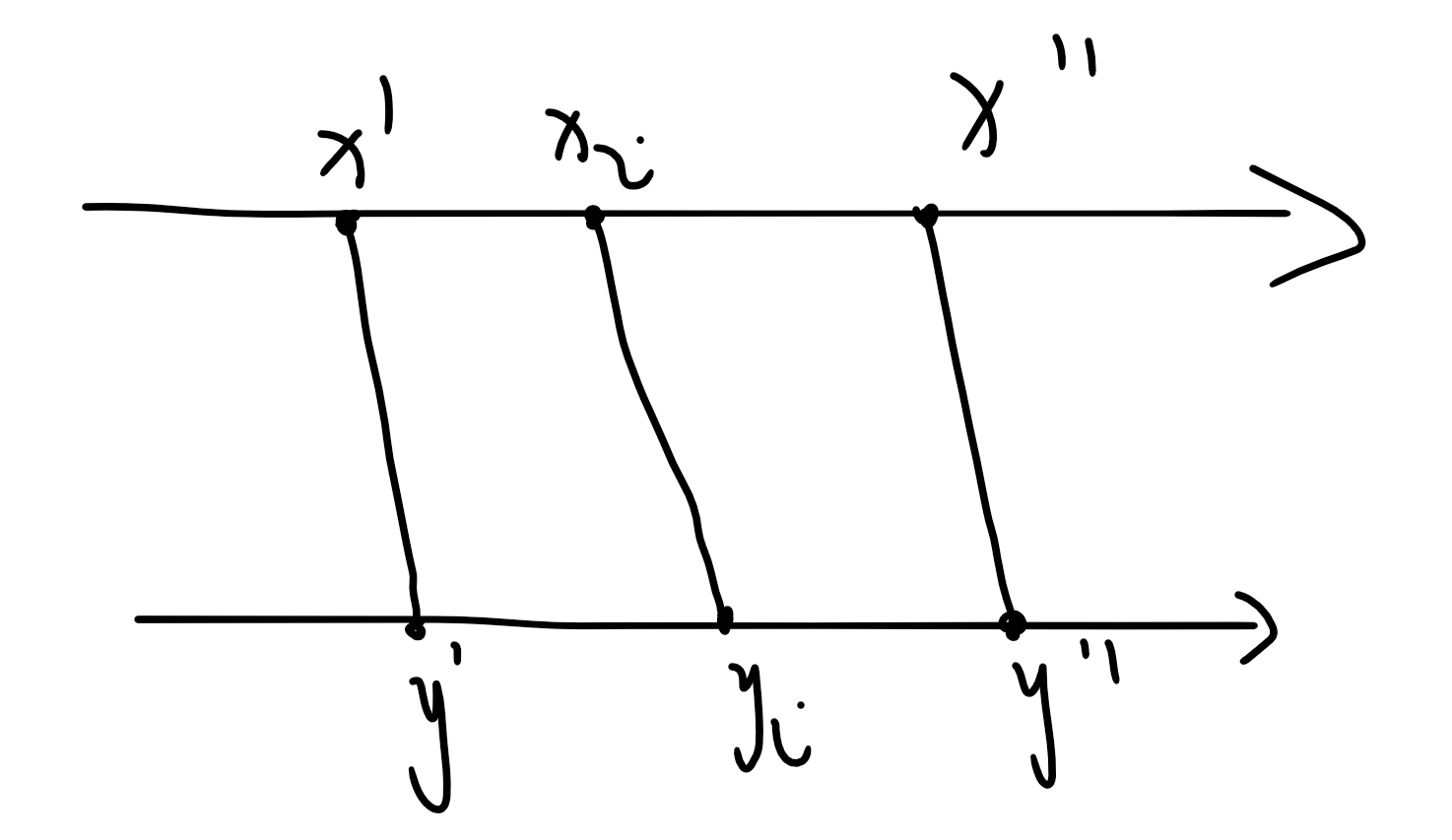
对于某一条边
来说:
对于所有边 ,则两条边不会有任何影响。
对于所有边 ,则两条边不会有任何影响。
上面两条比较显然,因为无论怎么定向,都不会形成新的强连通分量。

当出现这种红边 且 时,边一定是 更优。
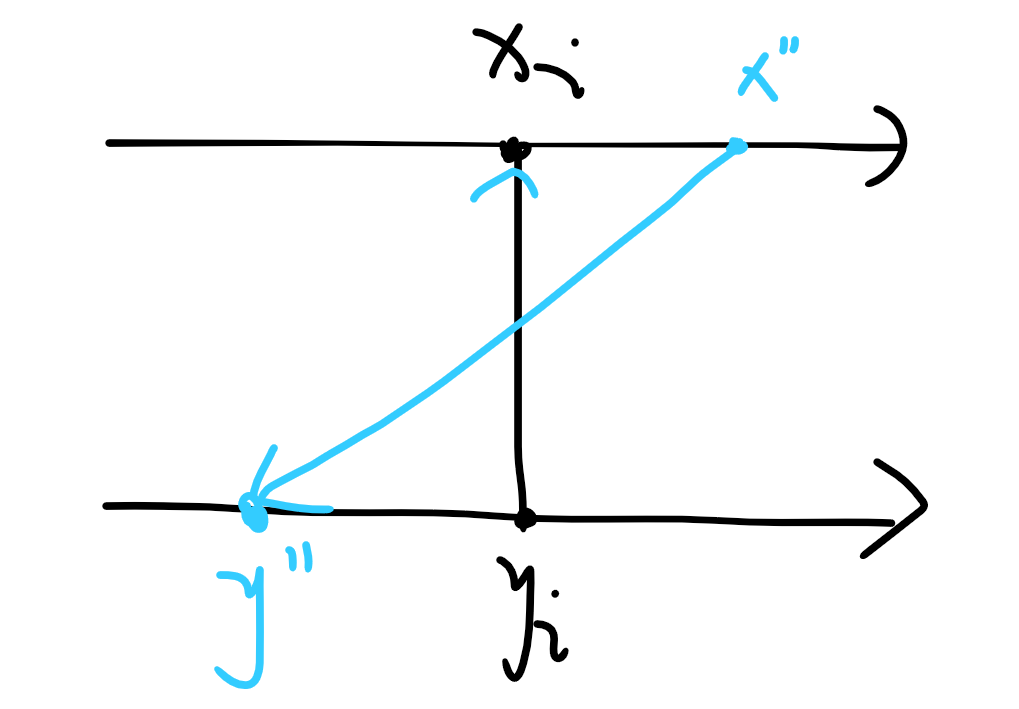
当出现这种蓝边 且 时,边一定是 更优。
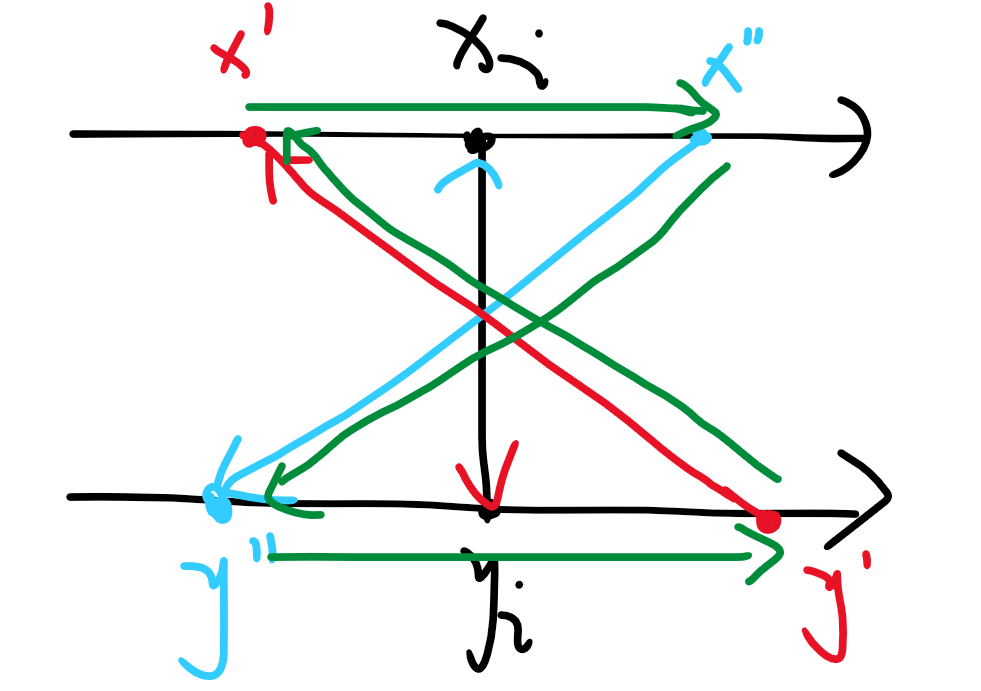
值得一提的是,当红蓝边同时出现时,第
条边已经不重要了,因为无论方向如何,此时一定会有一个更大的绿色强连通分量。
有了这几个观察,这道题似乎就不那么难了。
先将所有边排序,第一关键字为
从小到大,第二关键字为
从大到小。
则对于每一条边 ,红边只可能出现在它的前面,蓝边只可能出现在它的后面。
考虑按照
从小到大的顺序,指定边
的方向。
设 为前 条边中,从下到上连的所有边中,最大的
(若不存在这种边,则 )。
分两种情况分类讨论。
若 ,则 有红边,则边方向为 。
显然,若
之后没有蓝边,此决策为最优决策;若 之后有蓝边,根据上面的讨论,一定会出现
“绿色”循环, 的两种决策等价。
若 ,则 一定没有红边,则边方向为 ,并令 。
显然,若
之后有蓝边,则此决策为最优决策;否则, 既没有蓝边也没有红边,
不会对答案造成任何影响,两种决策等价。
这两种情况下,我们做的决策都是全局最优决策,所以一定可以使得强连通分量个数最少。
特别地,你会发现 (虽然我们并没有用到这个性质
方案构造完了,随便 tarjan 一下答案就出来了。
时间复杂度 。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
| #include<bits/stdc++.h>
using namespace std;
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
template<const int N,const int M>
struct graph
{
int head[N+5];
int t[M+5];
int x[M+5];
int cntm;
graph(){ cntm=1;}
inline void clear(int n=N)
{
cntm=1;
for(int i=1;i<=n;i++) head[i]=0;
}
inline void ad(int u,int v)
{
cntm++;
t[cntm]=v;
x[cntm]=head[u];
head[u]=cntm;
}
inline void add(int u,int v)
{
ad(u,v);
ad(v,u);
}
inline int st(int num){ return head[num];}
inline int to(int num){ return t[num];}
inline int nx(int num){ return x[num];}
};
graph<400000,800000>g;
struct node
{
int x,y;
int id;
}a[200001];
int sta[400001],top;
int qans[200001];
int dfn[400001];
int low[400001];
bool in[400001];
int n,m,q;
int tot;
int tim;
void dfs(int num)
{
low[num]=dfn[num]=++tim;
sta[++top]=num,in[num]=1;
for(int i=g.st(num);i;i=g.nx(i))
{
int p=g.to(i);
if(!dfn[p])
{
dfs(p);
low[num]=min(low[num],low[p]);
}
else if(in[p]) low[num]=min(low[num],dfn[p]);
}
if(low[num]!=dfn[num]) return ;
int now;tot++;
do
{
now=sta[top--],in[now]=0;
}while(now!=num);
}
int main()
{
n=read(),m=read(),q=read();
for(int i=1;i<n;i++) g.ad(i,i+1);
for(int i=1;i<m;i++) g.ad(i+n,i+n+1);
for(int i=1;i<=q;i++)
{
a[i].x=read(),a[i].y=read();
a[i].id=i;
}
sort(a+1,a+q+1,[](node a,node b)
{
if(a.x!=b.x) return a.x<b.x;
return a.y>b.y;
});
int now=0;
memset(qans,-1,sizeof(qans));
for(int i=1;i<=q;i++)
{
if(now>=a[i].y)
{
qans[a[i].id]=0;
g.ad(a[i].x,n+a[i].y);
}
else
{
qans[a[i].id]=1;
g.ad(n+a[i].y,a[i].x);
now=a[i].y;
}
}
for(int i=1;i<=n+m;i++) if(!dfn[i]) dfs(i);
printf("%d\n",tot);
for(int i=1;i<=q;i++) printf("%d ",qans[i]);
return 0;
}
|
感谢观看!



