小清新思维题,但并不简单
教练留的作业题,卡了我一下午
题目链接
题意
现在二维平面上有 个点,第
个点坐标是 ,每一个点有存在和不存在两种状态。
显然全局一共有
种状态,求所有状态下,。
任意两点不重合,三点不共线
题解
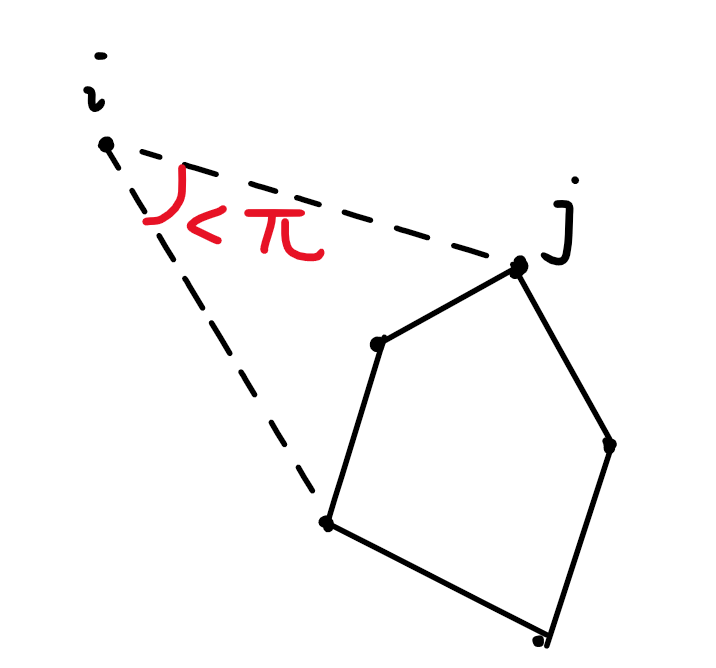
凸包内有多少点不好算,考虑对于每一个点算出,有多少种情况,这个点不在凸包内。
首先,若一个点 不在凸包内,则
一定没有被选(废话
再枚举一下,
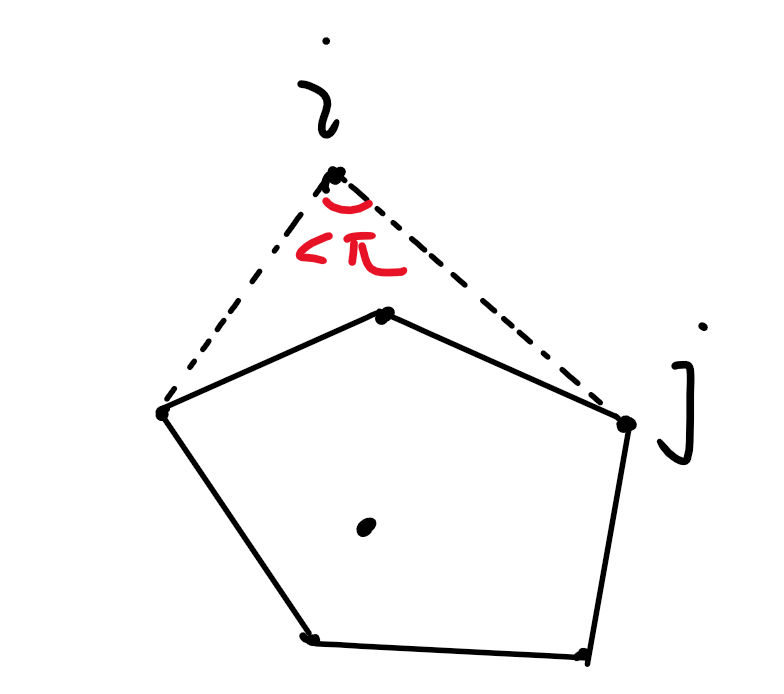
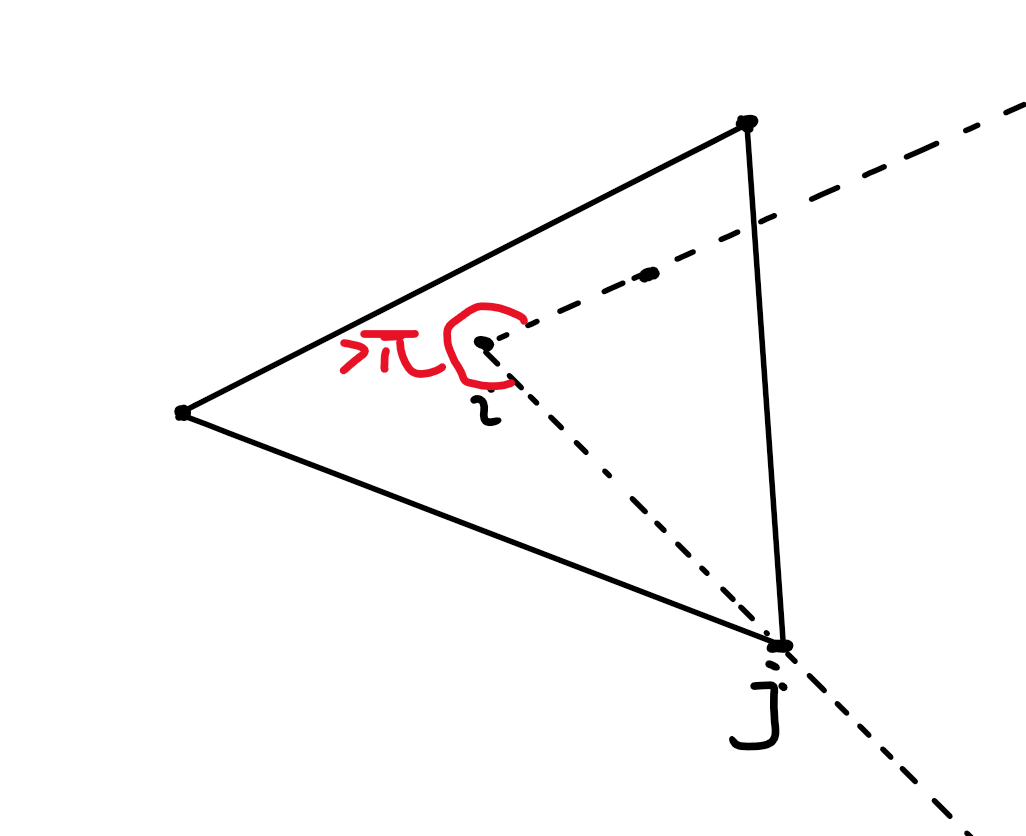
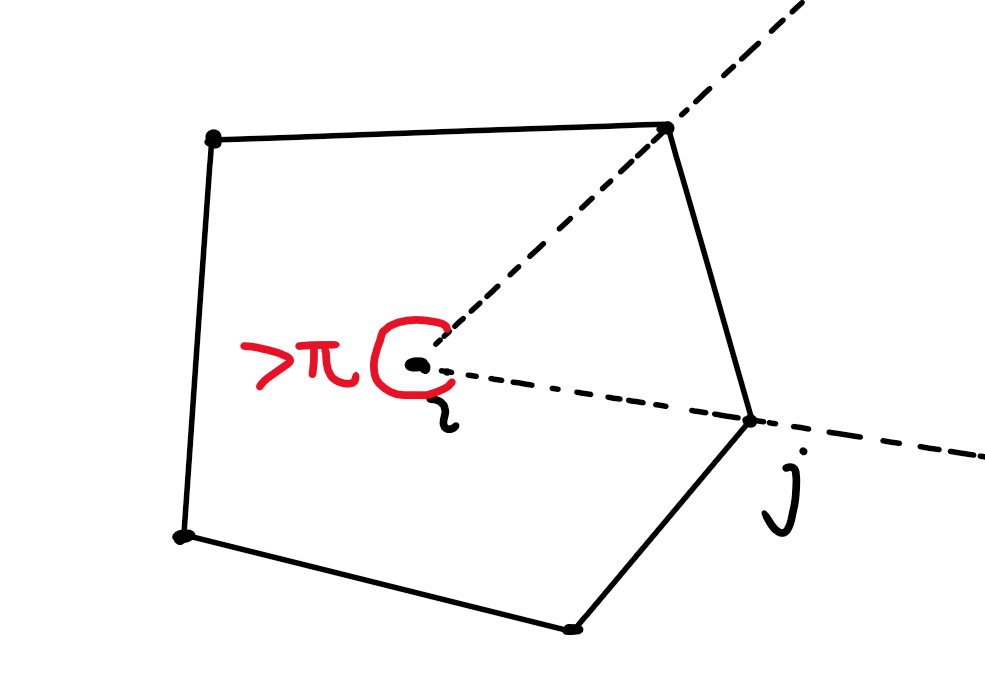
和这个凸包的第一条切线(顺时针)切在了哪个点 上,那么角度最大点一定不会超过 。
所以我们枚举一个点 ,将所有点按照极角排序。
然后枚举点 ,双指针可以得到一个点 ,使得它是最后一个,和 极角相差不超过 的点。
则点 必须选, 这些点可选可不选,就可以算出 不位于凸包内的方案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
|
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
using ld=long double;
const ld PI=acos(-1);
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
const int mod=1000000007;
ll p[2001];
ld d[2001];
int x[1001];
int y[1001];
int n,c;
inline ll qow(ll a,ll b)
{
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
int main()
{
n=read(),p[0]=1;
for(int i=1;i<=n;i++) x[i]=read(),y[i]=read(),p[i]=p[i-1]*2%mod;
ll ans=(p[n]-1)*n%mod;
for(int i=1;i<=n;i++)
{
c=0;
for(int j=1;j<=n;j++) if(i!=j)
{
if(x[j]==x[i])
{
if(y[j]>y[i]) d[++c]=90,d[++c]=450;
else d[++c]=270,d[++c]=630;
}
else
{
ld T=(ld)(y[j]-y[i])/(x[j]-x[i]);
ld D=atan(T)/PI*180;
if(x[j]<=x[i]) D+=180;
if(D<0) D+=360;
d[++c]=D,d[++c]=D+360;
}
}
sort(d+1,d+c+1);
int lst=1;
for(int i=1;i<n;i++)
{
while(d[lst]-d[i]<=180) lst++;
ans=(ans+mod-p[lst-i-1])%mod;
}
}
printf("%lld\n",ans);
return 0;
}
|
感谢观看!