Wuyanru's blog
0%

[CF2039F] Shohag Loves Counting

发表于 分类于 ，

你这 E 和 F 怎么难度相差这么大啊。

但是我感觉可能我 F1 就差一点啊。

题目链接 和 题目链接。

题意

对于一个长度为 的序列 ，定义 为，所有长恰好为 的区间，的区间最大值，的 。

称这个序列是好的，当且仅当对于所有 ，有 。

求有多少好的序列（长度没有限制），满足其中所有元素都为 中的整数。

easy ver.：。

hard ver.：。这里没有 限制喵。

题解

先来看 F1。

首先能发现一些东西，令 表示所有长度为 的区间最大值，来自多少个不同的位置。

那么可以发现一定有 ，因为如果有一个位置，是一个长度为 的区间最值，那么他一定是一个长度为 的区间最值。

那么就还可以知道，对于一个好的序列一定有 ，因为如果有 ，应该也会有 ，这就不合法了。

这相当于是，对于一个 来说，恰好有一个位置，是一个长为 的区间的最大值，但不是长度为 的区间最大值。

这也说明了 。

考虑我们已经知道了 里有哪些元素，但是不知道他们的排列顺序，仅考虑 的要求，可以有多少种排列顺序。

可以发现，这个序列一定是形如 先下降再上升这个样子的，如何证明呢。

考虑如果有两个“谷”的位置，那么在 的时候就有 了，这是不合法的。

而如果这个序列只有一个“谷”，那么就肯定只能是先下降再上升这个样子。

所以排列 的顺序恰好有 种方案。

那么也就是说，我们只需要计算出升序的 方案数，最后给方案数乘上 就好了。

先不考虑系数问题，我们现在需要求出这样一个问题：

给定 ，需要求出有多少序列 ，满足：

  1. 升序且最大值不超过 ，即 ；
  2. 后缀 gcd 互不相同，即令 ，有 。

这看起来就可以 dp，令 表示有多少序列，第一个值是 ，所有数的 gcd 是 。

边界状态是对于 有 。

考虑 可以从哪里转移过来，枚举后面所有数 gcd 为 ，那么新的 gcd 是 。

那么所有的 都可以转移到 。

前缀和优化一下，直接转移就能做到 ，怎么没有一个 F0 啊。

我们注意到 是 的因数，那么是否可以枚举 进行转移呢。

考虑令 表示所有 的和， 表示所有 的和。

那么按照从大到小的顺序枚举 ，然后枚举 ，考虑 可以从哪里转移。

可以发现，它可以从 转移过来。

但是有一个问题，就是此时可能会算重，假如一个状态可以转移到 ，那么他也会被算到所有 的因数里面，这就算重了。

但是这里处理比较简单，直接从大到小枚举每一个数字，让它的因数减掉它即可。

考虑复杂度，枚举 是 的，容斥和转移 的部分都是 的。

所以总复杂度是 。可以通过 F1。

等等你那个 的系数怎么飞了。

其实系数只需要在，每一次新添加一个数字的时候，给方案数 就好了。

代码。

再来看 F2。

这次没有了 的限制，我们从大到小的 dp 肯定就做不了了。

但是这里有一个很自然的解决方法，就是将原来的 dp 倒着转移。

什么叫倒着转移呢？

原来的 dp，边界为 ，可以从 转移到 ，最终答案为所有 的和。

现在我们把他全部反过来。

初始状态为所有 ，可以从 转移到 ，最终答案为所有 的和。

具体一点，现在的 表示如果现在有一个序列，第一个元素是 ，并且整个序列的 gcd 为 。

现在需要往这个序列前面添加若干元素（可以不添加），使得这个序列合法，前面有多少添加的方案。

这样我们就只需要一开始跑一遍 dp，然后统计 的前缀和即可。

具体的 dp 转移直接把上面的全部反着抄过来就好了。

可以将原来的 dp 过程看作，一张有向图，求的是起点到终点有多少种不同的路径。

现在我们将所有的边都反向，边权不变，求出终点到起点有多少种不同路径，两个问题答案显然相同。

想要推转移的话，把原来的图画出来就非常好反向了。

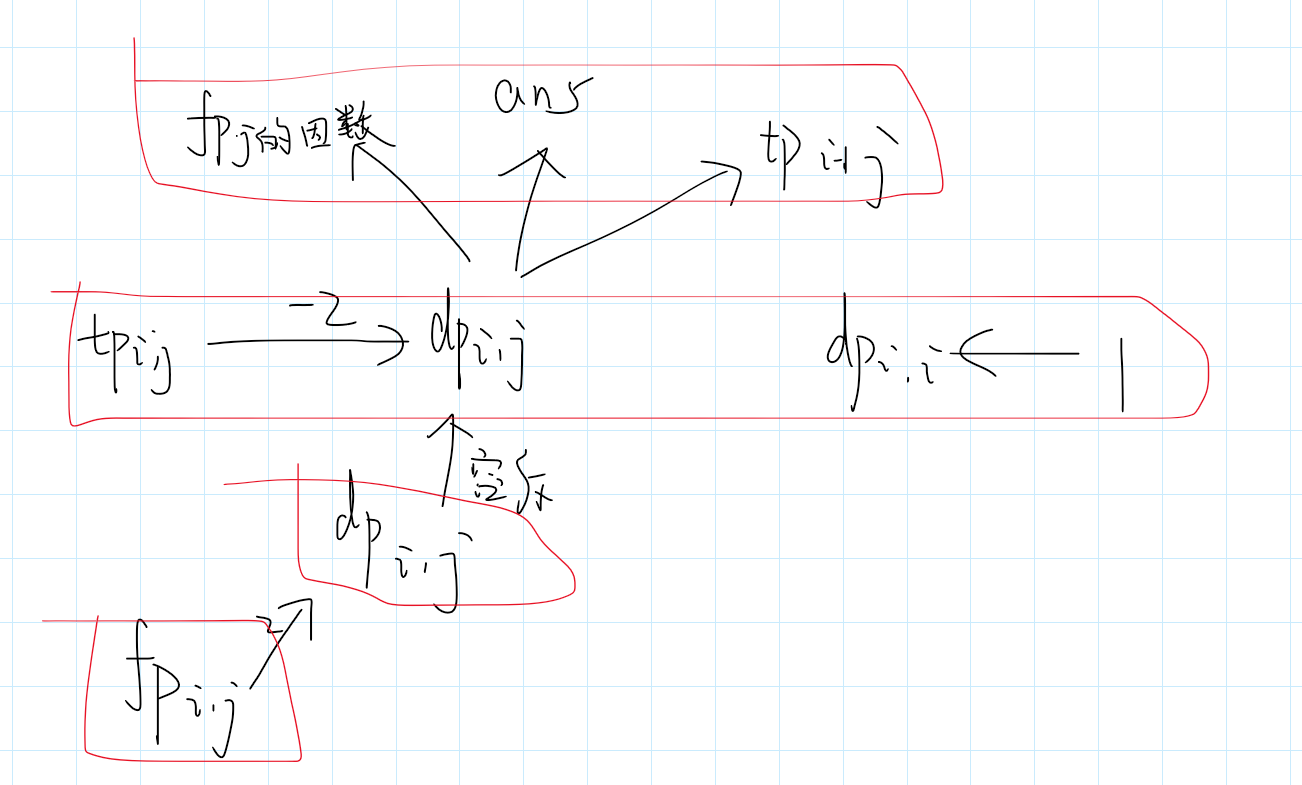
令 ，那么直接改一下就能做到 。

代码。怎么就比时限少了十几毫秒的。

但是其实还能优化一点，可以发现代码中有两处复杂度瓶颈。

而这两处复杂度瓶颈都可以通过 SOS DP 进行优化（其实就是，把质数当成进制的高维前缀和）。

令 表示数字 的不同质因数个数，则可以改到 。

代码。其实没快多少。