哎,人类智慧题。
从来没有见过这样的题,写篇题解纪念之。
题目链接。
题意
现在有一个大小为
的网格,格子有三种,海水、火山与岛屿。
定义一个格子的权值,为到所有火山的曼哈顿距离的最小值。
现在有 次询问,每一次给定格子
,你现在需要从
这个格子出发,每一次走到相邻的非岛屿的四连通格子内,包围整个岛屿,并回到格子
(可以经过相同格子)。
对于每一组询问,你的路径的权值,是所有经过格子的权值的最小值,你需要输出路径权值的最大值。
其中,包围的定义是,不存在一条从岛屿出发的八连通的路径,可以不经过你走到的格子,到达网格边界。
。
。
题解
既然要求路径的权值,不妨先把每一个格子的权值求出来。
这一步是简单的,可以使用多源 bfs 在 的复杂度内求出。
考虑什么样的路径是合法的。
考虑从岛屿的边界为起点,引一条只经过格子边界(不经过岛屿边界),且终点在网格边界的简单折线(例如下图黑色折线)。
可以发现,任意一个可能作为答案的方案合法,当且仅当穿过了这条线奇数次(例如下图白线)。
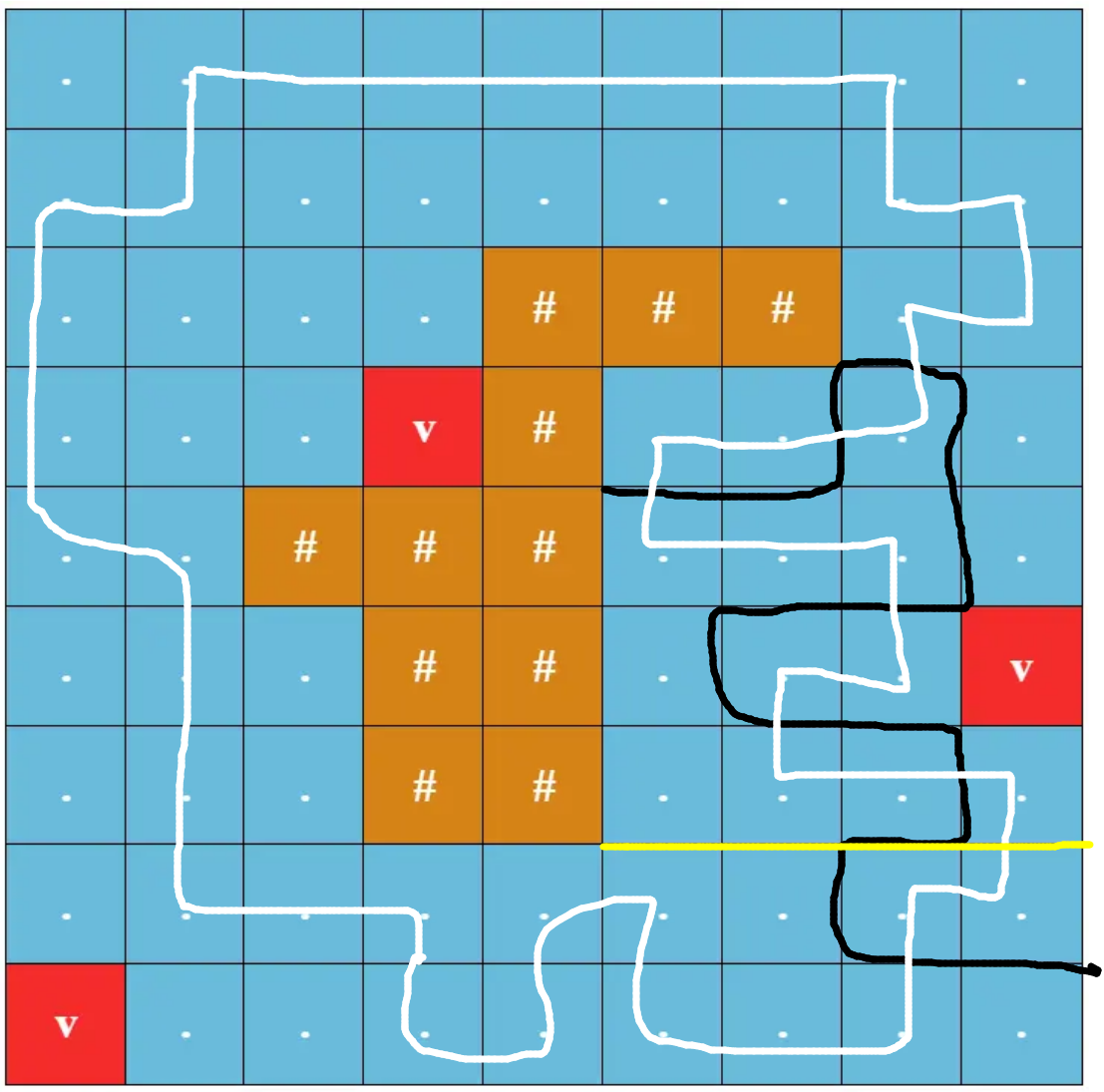
一个粗略的证明:
以上图黑色折线为例,可以发现,折线的一端在岛屿边界,而另一端在网格边界,这样整张图就从一个环形的结构,被黑线分成了一个链式的结构。
再来考虑任何一条合法路径(例如白线),我们先给它选一个方向(顺时针或逆时针,这里以顺时针举例)。
我们再给黑色折线的每一侧定一个方向,例如上下。
这个时候来观察白线与黑色折线的所有交点。
可以发现,白线被分成了若干段(废话,白线若没有经过黑线一定不合法)。
由于我们给白线定了方向,又给黑线定了上下侧的区别。
那么每一段白线都可以划分为以下四种类型之一:上侧到上侧、上侧到下侧、下侧到上侧、下侧到下侧。
例如,白线中最长的一段就是从下侧到上侧,特殊的,这个例子中整个白线中并没有出现上侧到下侧。
回到证明中,假设白线被黑线分了
段,那么就会有
个交点,上侧与下侧在所有线段类型中便会各出现 次。
这时,如果
是奇数,那就必然会出现上侧到下侧和下侧到上侧中的至少一种。
这时候证明就很简单了,因为白线连成了环状,所以只要出现上述两种情况中的一种,岛屿就一定被“包围”。
现在我们就证明了,穿过黑线奇数次的方案,一定是合法的。
那么穿过黑线偶数次的方案呢?它们一定不合法吗?
答案是,这些方案可能合法,但没有必要管他们。
来看这两种情况,红线都穿过黑线偶数次,但它们都是合法方案(加粗点为起点)。
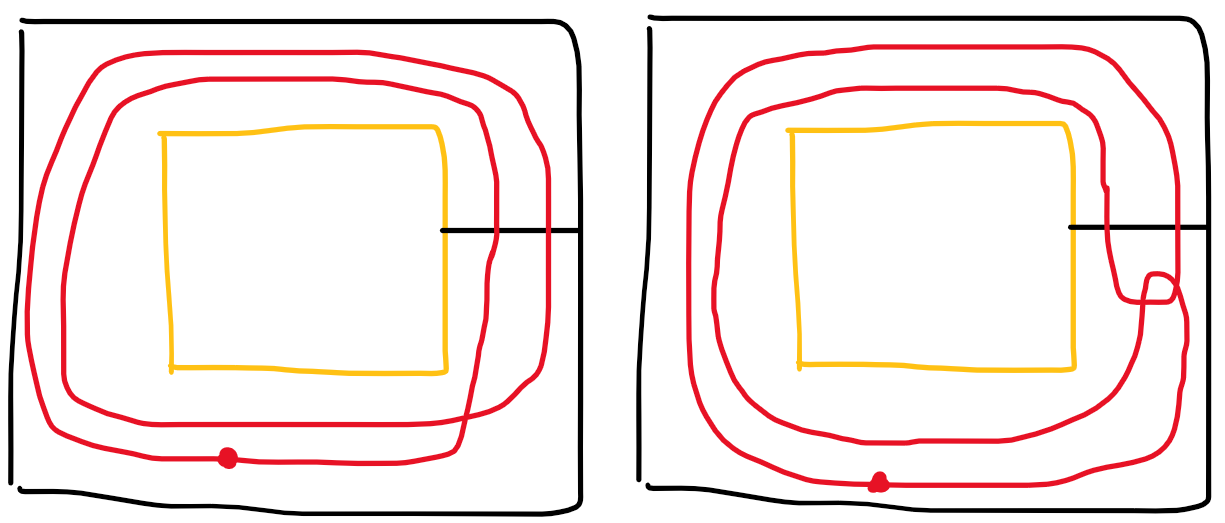
容易发现,如果这种情况合法,那么上侧到下侧、下侧到上侧出现次数和必然
,那么整个路径就必然有自相交的部分。
既然有相交的部分,我们就可以化简。
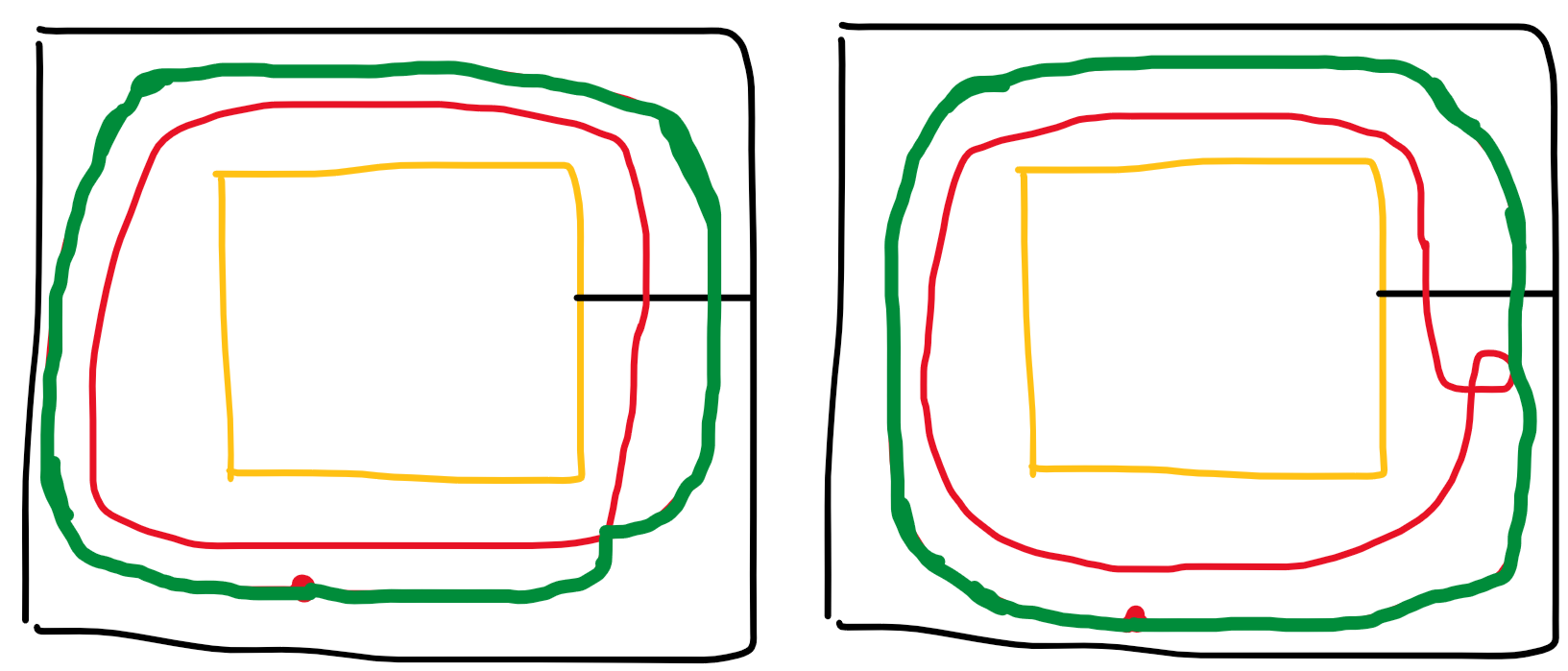
只保留绿色部分,答案一定不劣,并且经过格子数量变少。
一直化简下去,红线一定能变为只穿过黑线奇数次,并且答案不劣于原来的方案。
所以经过黑线奇数次的答案要么不合法,要么没必要统计。
那么如何取黑线呢?可以参照第一张图,从岛屿边缘直接引一条普通线段即可(那条黄线)。
现在我们知道了什么情况是合法的,考虑如何计算答案。
那么现在的问题就是,对于每一组询问的点 ,我们需要找一条路径,使得它穿过了黑线奇数次,并回到
,需要最大化这条路径的权值。
首先想暴力怎么做(首先设
表示格子 的权值)。
我们可以令
分别表示,现在在点 ,经过了黑线奇数次还是偶数次,最大权值是多少。
那么答案就是 。
我们可以令初始情况为 ,然后跑一个最短路即可。
这样单组的复杂度是
的,可以通过 F1。
这个时候我们可以发现一些有趣的事情,例如对于所有询问来说,我们建的图都长得一样。
我们还可以改变一下求的东西,不难发现 表示的其实是,找出一条起点为
且终点为
的路径,使它路径上点的权值最小值最大。
这不是我们重构树能干的事吗?
所以我们只需要一开始把最大生成树的重构树建出来(一条边 边权的定义是 )。
之后对于所有的询问 ,我们只需要查出点 与 的 LCA 即可。
时间复杂度是 ,其实
完全可以消掉,但是加上也能过。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
| #include<bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f3fll
#define debug(x) cerr<<#x<<"="<<x<<endl
using namespace std;
using ll=long long;
using ld=long double;
using pli=pair<ll,int>;
using pi=pair<int,int>;
template<typename A>
using vc=vector<A>;
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};
struct node
{
int u,v;
int w;
node(int u=0,int v=0,int w=0):u(u),v(v),w(w){}
}e[1200001];
int fa[1200001][22];
int dep[1200001];
int w[1200001];
int f[1200001];
int dis[300005];
char s[300005];
int rx,ry;
int n,m,q;
int cntm;
int cnt;
inline void bfs()
{
queue<int>que;
memset(dis,0x3f,sizeof(dis));
for(int i=0;i<n*m;i++) if(s[i]=='v') dis[i]=0,que.push(i);
while(!que.empty())
{
int u=que.front();que.pop();
int x=u/m,y=u%m;
for(int i=0;i<4;i++)
{
int vx=x+dx[i],vy=y+dy[i];
if(vx<0||vx>=n||vy<0||vy>=m) continue;
int s=vx*m+vy;
if(dis[s]>dis[u]+1) dis[s]=dis[u]+1,que.push(s);
}
}
}
inline int find(int num)
{
if(f[num]==num) return num;
return f[num]=find(f[num]);
}
inline int lca(int u,int v)
{
if(dep[u]<dep[v]) swap(u,v);
for(int i=20;i>=0;i--) if(dep[u]-(1<<i)>=dep[v]) u=fa[u][i];
if(u==v) return u;
for(int i=20;i>=0;i--) if(fa[u][i]!=fa[v][i]) u=fa[u][i],v=fa[v][i];
return fa[u][0];
}
int main()
{
n=read(),m=read(),q=read();
for(int i=0;i<n;i++)
{
scanf("%s",s+i*m);
for(int j=ry;j<=m;j++) if(s[i*m+j]=='#') rx=i,ry=j;
}
bfs();
for(int i=0;i<n;i++) for(int j=0;j<m;j++) if(s[i*m+j]!='#')
{
int v=i*m+j;
if(i&&s[v-m]!='#')
{
if(i==rx&&j>=ry)
{
e[++cntm]=node(v+n*m,v-m,min(dis[v],dis[v-m]));
e[++cntm]=node(v,v-m+n*m,min(dis[v],dis[v-m]));
}
else
{
e[++cntm]=node(v,v-m,min(dis[v],dis[v-m]));
e[++cntm]=node(v+n*m,v-m+n*m,min(dis[v],dis[v-m]));
}
}
if(j&&s[v-1]!='#')
{
e[++cntm]=node(v,v-1,min(dis[v],dis[v-1]));
e[++cntm]=node(v+n*m,v-1+n*m,min(dis[v],dis[v-1]));
}
}
cnt=2*n*m-1;
sort(e+1,e+cntm+1,[](node x,node y){ return x.w>y.w;});
for(int i=0;i<=cnt;i++) f[i]=i;
memset(fa,-1,sizeof(fa));
for(int i=1;i<=cntm;i++)
{
int u=find(e[i].u),v=find(e[i].v);
if(u==v) continue;
cnt++,w[cnt]=e[i].w;
f[u]=f[v]=f[cnt]=cnt;
fa[u][0]=fa[v][0]=cnt;
}
for(int i=cnt;i>=0;i--)
{
for(int j=0;fa[i][j]>0;j++) fa[i][j+1]=fa[fa[i][j]][j];
if(fa[i][0]>0) dep[i]=dep[fa[i][0]]+1;
}
for(int i=1;i<=q;i++)
{
int x=read()-1,y=read()-1;
int v=x*m+y;
printf("%d\n",w[lca(v,v+n*m)]);
}
return 0;
}
|
感谢观看!


