一个很难的计数,但是分析过程非常的自然。
题目链接。
题意
给定一张 个点 条边的无向图,现在需要给每一条边染上
这三种颜色之一。
称一组染色方案是好的,当且存在简单路径,使得路径上这 种颜色都存在。
简单路径指点不重复的路径,需要求出好的染色方案对 取模的结果。
。
题解
染色的总方案数是 ,大概直接能看出来,不合法的方案数更好算一些。
所以考虑先算出不合法的方案数,然后减一下。
不合法的方案即所有简单路径都至多含有 种颜色的方案。
先考虑判掉一些平凡的情况,例如整张图只有 种或 种颜色,这里的方案数是 。
称一种方案是坏的,当且仅当
种颜色都出现过,且不存在简单路径同时含有三种颜色。
那么现在只要算出坏方案的数量,问题就解决了。
来考虑,一个坏方案上,若存在一个简单环,环上同时出现了 种颜色,会发生什么。
可以发现,这个环的大小一定是 ,因为环长如果 ,一定可以找出一条简单路径含有 种颜色。
而若环的大小是 ,则因为有重复点,环内不能构成简单路径。
这样我们可以知道环上一定是
种颜色恰好有一个。
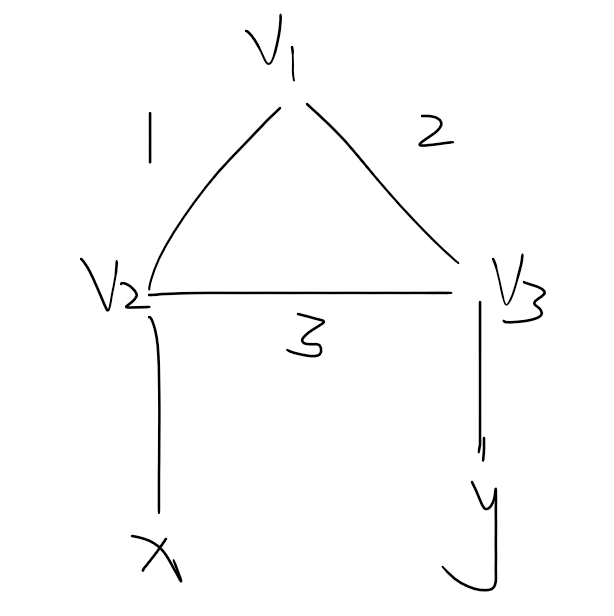
假设有两个不同点 分别连接了环上的两个点。
若 为 或 ,则可以直接找到一个含有 种颜色的路径,所以可以知道 为 。
同理可以知道 颜色为 ,但是这样 又是一条有 种颜色的路径。
所以这种情况一定不是坏方案。
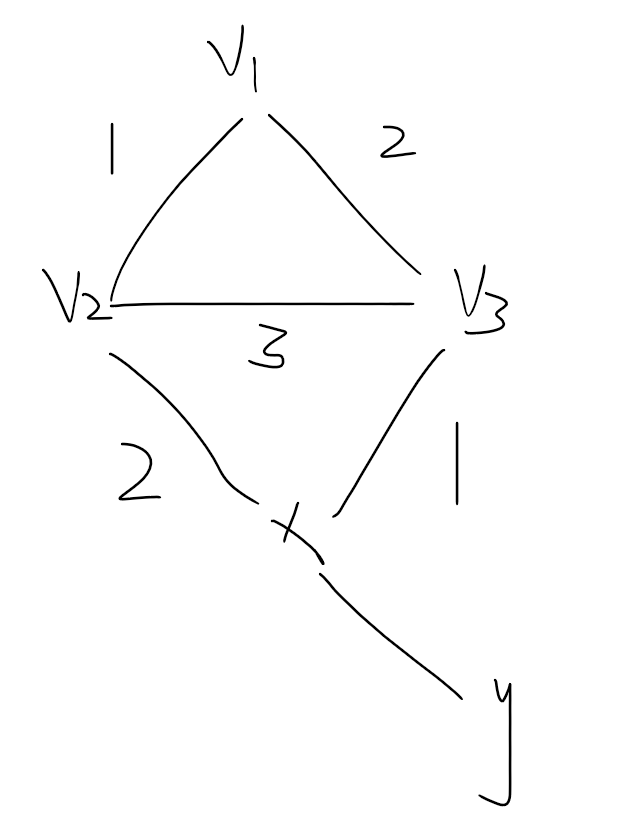
再考虑这种情况,若存在一个点
同时连接了环上两个点。
若此时 ,则图里至少还有一个点 ,根据上面的讨论知道若 与 有边则这不是坏方案。
所以
一定有边,可以发现此时这条边无论是什么颜色,这张图仍然不是坏方案。
那我们可以得到结论,对于一个 的坏方案,若存在一个环包含 种颜色,则:
- 这个环上恰好有 个点;
- 这个环上只有恰好一个点,与环外的点有连边。
对于
的情况可以直接暴搜。考虑剩下的情况如何计算。
对于
的情况,可以发现若存在一个环包含
种颜色,则环外所有边同色。
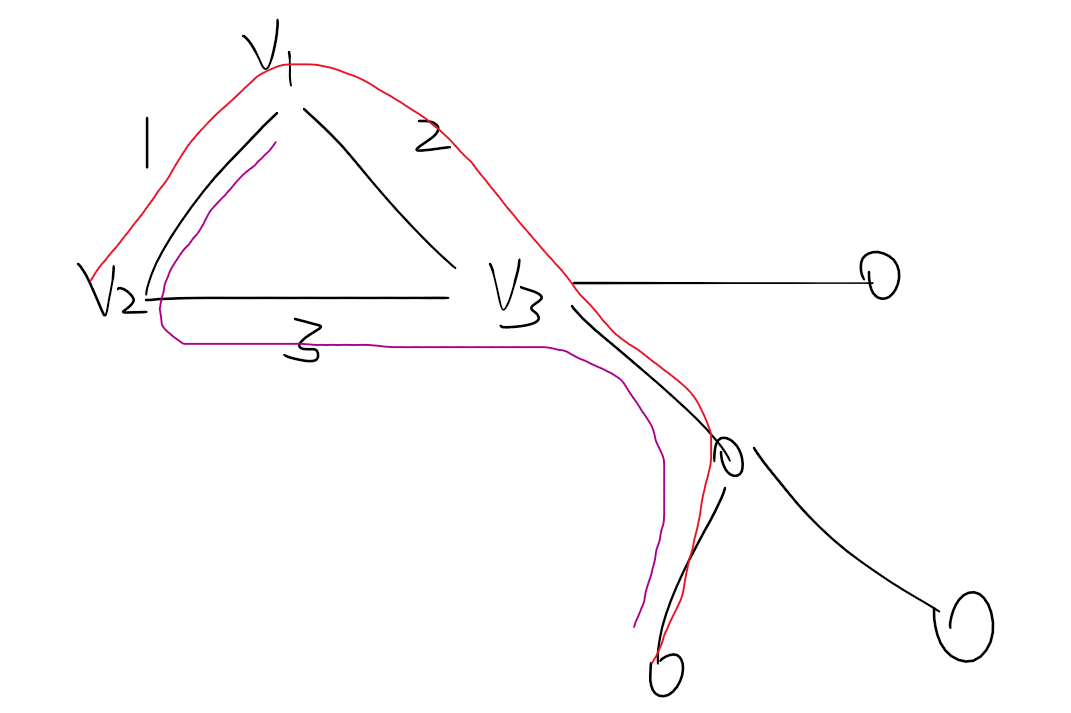
所以对于存在环包含
种颜色的坏方案数量是好算的。
设 为图中大小为
且只有一个点向外连边的的极大点双连通分量个数,则这部分方案数为 。
对于没有环存在
种颜色的情况,假设现在有一个环,恰好包含了两种颜色 。
因为坏方案要求三种颜色的边都要有,所以一定有一条环外的 边。
考虑分情况讨论。
第一种情况是,若存在一条
边不为这个环的弦:
那么一定存在这条
边到这个环的一条路径。
而我们知道环的大小至少是 ,那也就是说一定存在一条路径包含 种颜色,这是不合法的。
也就是说,一个坏方案的
边一定在环的弦上。
再考虑这么两种情况:
第一种情况是,弦将环分成的两部分,一部分只有 边,一部分只有 边。
容易发现这种情况不是坏方案,因为只需要选择这条 边,然后两端分别选择一个 边,就出现了 种颜色的路径。
对于剩下的情况,可以发现,这条
边与环上的某一部分形成了一个新的环。
而这个环包含了
三种颜色,这与我们的假设不符。
所以可以得到结论,对于没有环存在
种颜色的情况,一个坏方案的任意一个环上,一定不可能同时存在两种颜色。
再考虑剩下的情况,可以发现,这部分等价于,所有同一个点双连通分量上的边,颜色都相同。
考虑建出原图的圆方树,可以发现,坏方案等价于,存在一个“中心点”,这个中心点将整棵树分为了若干部分,每一部分的颜色全部相同。
这是好算的,随便弄一弄就好了。
这样就算出了坏方案的总数,减一下就能得到答案了。
时间复杂度 。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
| #include<bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f3fll
#define debug(x) cerr<<#x<<"="<<x<<endl
using namespace std;
using ll=long long;
using ld=long double;
using pli=pair<ll,int>;
using pi=pair<int,int>;
template<typename A>
using vc=vector<A>;
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
inline ll lread()
{
ll s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
const int mod=998244353;
int sta[200005],top;
ll dp[200001][4];
vc<int>g[200005];
vc<int>t[400005];
int dfn[200005];
int low[200005];
bool vis[6];
int col[6][6];
int n,m,c,tim;
ll ans;
inline bool check(int s,int sta)
{
if(vis[s]) return false;
if(sta==7) return true;
vis[s]=1;bool ans=false;
for(int i=1;i<=n;i++) if(col[s][i]!=-1) ans|=check(i,sta|(1<<col[s][i]));
vis[s]=0;
return ans;
}
inline bool sub1()
{
for(int i=1;i<=n;i++) if(check(i,0)) return true;
return false;
}
void sub1(int x,int y)
{
if(x==n+1)
{
if(sub1()) ans++;
return ;
}
if(y==n+1) sub1(x+1,1);
else if(col[x][y]!=10) sub1(x,y+1);
else
{
for(int i=0;i<3;i++) col[x][y]=col[y][x]=i,sub1(x,y+1);
col[x][y]=col[y][x]=10;
}
}
inline ll qow(ll a,ll b)
{
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
void dfs(int num)
{
dfn[num]=++tim,low[num]=tim;sta[++top]=num;
for(int p:g[num])
{
if(!dfn[p])
{
dfs(p);
low[num]=min(low[num],low[p]);
if(low[p]<dfn[num]) continue;
c++;t[num].push_back(c);int now;
do
{
now=sta[top--];
t[c].push_back(now);
}while(now!=p);
}
else low[num]=min(low[num],dfn[p]);
}
}
inline bool check(int s)
{
if(t[s].size()!=2) return false;
int cnt=0;
if(!t[t[s][0]].size()) cnt++;
if(!t[t[s][1]].size()) cnt++;
if(cnt==2) return true;
if(cnt==1&&t[1].size()==1&&t[1][0]==s) return true;
return false;
}
int main()
{
c=n=read(),m=read();
for(int i=1;i<=m;i++)
{
int u=read(),v=read();
g[u].push_back(v);
g[v].push_back(u);
}
if(n<5)
{
memset(col,-1,sizeof(col));
for(int i=1;i<=n;i++) for(int j:g[i]) col[i][j]=10;
sub1(1,1);
printf("%lld\n",ans);
return 0;
}
dp[0][0]=1;
for(int i=1;i<=n;i++) for(int j=1;j<=3;j++) dp[i][j]=(dp[i-1][j]*j+dp[i-1][j-1]*(4-j))%mod;
dfs(1);
for(int i=1;i<=c;i++)
{
if(i<=n) ans+=dp[t[i].size()+(i!=1)][3];
else if(check(i)) ans+=6;
}
ans+=3*(qow(2,m)-1);
ans=qow(3,m)-ans;
ans=(ans%mod+mod)%mod;
printf("%lld\n",ans);
return 0;
}
|


