感觉是好久之前看到的题,今天终于有勇气补了。
题目链接。
题意
对于一张连通图,定义它是好的,当且仅当其所有生成树都存在完美匹配。
给定 ,求有 个点的好的连通图数量。
,模数是输入的质数,
为偶数。
题解
首先考虑什么样的图是好的。
因为对于所有生成树来说,各个点双内部的方案是独立的,所以考虑对一个点双进行分析。
对于一个点双,设 表示
这个点外面挂了多少个其他点双的点(不包括 这个点)。
那么可以知道,若 是偶数,则
一定要在这个点双内部照匹配点,否则要在点双外部找匹配。
接下来分类讨论一下。
第一种情况:
假设这个点双内部同时出现了
为偶数和
为奇数的点,会发生什么。
首先,因为点双内部肯定是连通的,所以此时一定存在一条边,满足这条边两侧的点
奇偶性不同。
而由于我们找的是一个点双,所以删掉那个
为偶数的点之后,整张图仍然连通(至少存在一个生成树)。
那么就可以直接构造出来一棵生成树,使得这个
为偶数的点,在这个点双内只连了一条边(另一侧是那个 为奇数的点)。
这显然是不合法的,所以可以知道,一个点双内部,不能同时存在 为奇数和 为偶数的点。
第二种情况:
如果这个点双内部只有
为奇数的点。
显然,所有点都只会向外找匹配,这个点双内部什么影响都没有。
第三种情况:
如果这个点双内部只有
为偶数的点。
那么显然,所有的点都要在这个点双内部找匹配。
我们来看看,假如一个点,度数至少是 ,会发生什么。
假设有一个点 度数至少是
,取其连边中编号最小的点,设为
。
不妨假设,这部分的构造中,生成树的根均为 。
首先按照之前的分析,我们可以构造出一棵生成树 ,满足 在这棵树里面之和 连边。
我们还可以构造出一棵生成树 ,使得其为 删掉边 再加上边 。
如果整个点双要合法,则
都需要有完美匹配,这说明
的其他所有子树都存在完美匹配(不算本身的子树大小为偶数)。
那么我们可以再构造出一棵树 ,满足 和 这写点有连边,在 中
与其父亲的连边都不存在,其余边完全一样的树。
可以发现,此时
子树内都是完美匹配,所以
都需要和
匹配,这就不合法了。
偷一张 AT 官解的图上来:

所以说,在这种情况中,所有的点度数都必须 。
也就是说整张图要么是一个大环,要么只有两个点中间连一条边。
那么我们现在就可以分析出合法图的结构了:
首先这张图最基本的部分是
个点组成了若干个环与若干条单边。
然后再在不同的部分中间加边(形成新的点双),直到连成了一张连通图。
现在我们就可以考虑如何进行计数了。
但在这之前,我们需要解决一个稍微简单一点的问题,如何计算 个点的点双连通图个数。
首先先来计算
个点的连通图数量,设答案为 。
首先, 个点的图总数为 ,再减掉不连通的图方案数就是连通图总数。
直接枚举点
所在连通块大小即可,得到 。
这可以在
的时间内计算。
再来考虑如果对点双连通图计数,设 个点的连通图中,有 个点双的图有 种。
(特殊的,当
时整张图为一个单点,我们定义其有一个点双)。
那么显然,,所以我们只需要考虑如何计算
。
不难发现一张图有
个点双,相当于其圆方树中有
个方点,不妨画一个图出来看看。
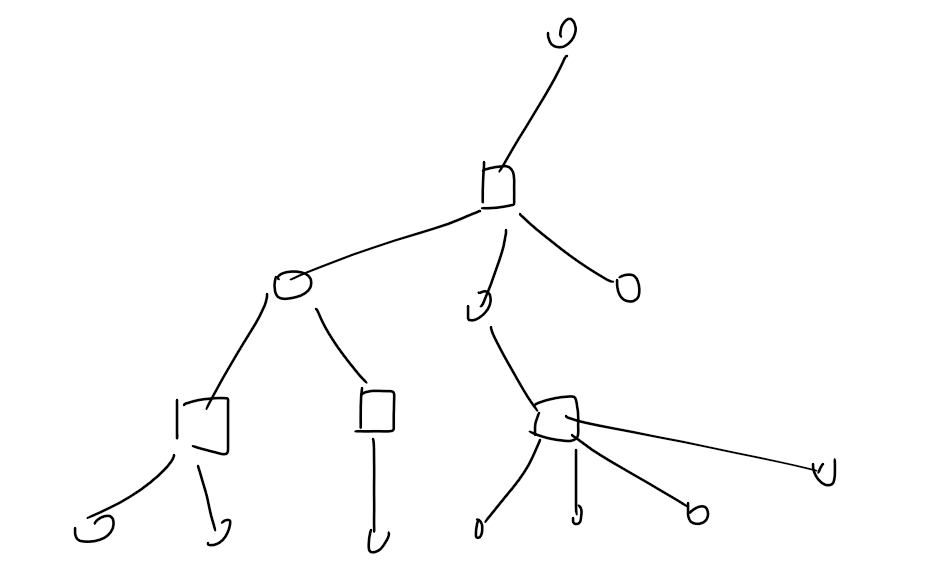
(似乎可以直接对着这个圆方树 dp,但是直接 dp 的话我好像只会 )。
我们先固定
号点为根,然后再给每一个方点一个编号(后面方案数除掉 即可)。
设编号为 的方点有 个儿子,那么有 和 。
考虑如果给定一组
的取值,能否算出其对应的方案数。
首先需要把 这 个圆点分配给 个方点,方案数是 。
第 个点双有 个点,所以还要乘上点双的方案数
。
然后我们要给每一个方点找一个父亲(其实是找爷爷),其挂在第 个方点下面的方案数是 。
由于还有直接连到根下面的情况,不妨认为还有一个 号方点只有 号圆点一个儿子(,所以后面有 )。
可以发现连边的方案数不好计算,但是考虑一个不同的问题。
现在有 个点,第 个点有点权 。
一条边 的权值是 ,一棵树的权值是所有边权的乘积。
问所有树的权值之和。
不难发现,这是个经典问题,答案是 。
而我们发现这个问题和我们上面要算的方案数几乎没有区别。
我们要算的东西只有父亲那一端有代价,而这个问题是两条边都有代价。
不同的部分儿子的部分没有代价,而每一个点显然有恰好一条边作为儿子,所以我们只需要给总权值除掉
即可。
总结,若给定一组 ,则方案数为
。
(可能会算错的地方:一共有
个点所以 的指数是 )(还有这里官解好像写错了)。
然后我们直接对这个 跑 dp
就好了,复杂度是 的。
现在回到原题,我们需要计算合法的图方案数。
首先我们需要将 个点分成
个部分,每一个部分都是一条单边或者一个偶数个点的环。
然后这
个部分需要拼成一整个连通块,考虑这样的过程:
每一次调出
个部分,强制编号为
的部分必须拿出,加边让这些部分形成一个连通的新部分,编号为 。
不断重复使得只剩下一个部分,此时整张图连通,不难发现这样计数的过程是不重不漏的。
那么显然,在一次加边的过程中,每一个部分只会存在一个点,有向外的连边,不然会爆炸。
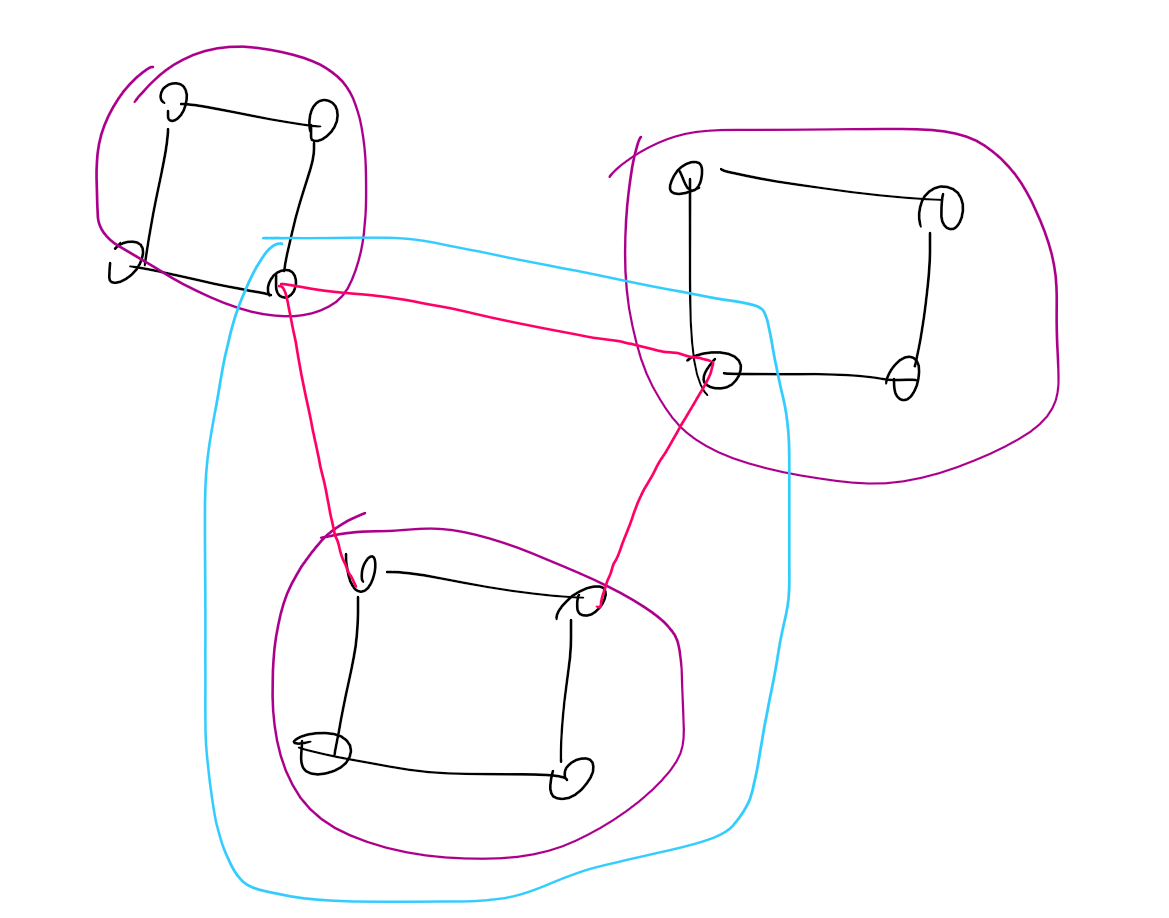
(原来存在三个部分(紫色),新加入三条边(红色),形成了新的点双(蓝色))。
那么考虑方案数如何计算。
假设这 个部分又形成了 个点双,考虑和上面类似的思路:
首先,有 个圆点,第 个圆点代表一个有 个小点的部分;还有 个方点,编号为 。
号方点是我们虚构出来的,和
号圆点一起代表整棵树的根(我们强制小点 需要在 号圆点内,其余不强制)。
所有方点至少都要有一个圆点作为儿子,除了
号方点的其余所有方点需要找一个方点作为爷爷。
考虑方案数,首先若确定了树的形态,要将所有圆点连成点双,所以对于每一个方点首先有
的贡献。
其次还要考虑每一个点在一个点双内部,选哪个点往外连边。
对于一个圆点,其向父亲只有一条边,所以这部分相当于所有部分的大小之积(编号为
的部分不算)。
对于向儿子的方案数,因为儿子是方点,所有可以直接考虑每一个方点爷爷是谁,也就是说我们不关注每一个方点父亲是谁,只关注爷爷是谁。
这样的话,一个方点到其爷爷的方案数,就是其爷爷下面的所有圆点内部,小点的个数和。
考虑预处理一个
表示一个方点下面有
个小点的方案数权值和。
假设第 个方点下面挂了
个小点,则方案数(不考虑分配小点给方点)大概是 。
(这里需要注意可能会出现
的情况)。
那么瞎 dp 一下就好了。
时间复杂度 。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
| #include<bits/stdc++.h>
#define inf 0x3f3f3f3f3f3f3f3fll
#define debug(x) cerr<<#x<<"="<<x<<endl
using namespace std;
using ll=long long;
using ld=long double;
using pli=pair<ll,int>;
using pi=pair<int,int>;
template<typename A>
using vc=vector<A>;
template<typename A,const int N>
using aya=array<A,N>;
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
inline ll lread()
{
ll s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
ll p2[250005];
ll dp[505][505];
ll g[505][505];
ll C[505][505];
ll jc[505],inv[505];
ll f[505],h[505];
int n,mod=998244353;
inline ll qow(ll a,ll b)
{
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
int main()
{
n=read(),mod=read();
for(int i=0;i<=n;i++)
{
C[i][0]=C[i][i]=1;
for(int j=1;j<i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
p2[0]=1;
for(int i=1;i<=n*n;i++) p2[i]=p2[i-1]*2%mod;
f[0]=jc[0]=inv[0]=1;
for(int i=1;i<=n;i++)
{
f[i]=p2[i*(i-1)/2],jc[i]=jc[i-1]*i%mod,inv[i]=qow(jc[i],mod-2);
for(int j=1;j<i;j++) (f[i]-=C[i-1][j-1]*f[j]%mod*p2[(i-j)*(i-j-1)/2])%=mod;
f[i]=(f[i]%mod+mod)%mod;
}
dp[0][0]=1;
for(int i=1;i<=n;i++)
{
g[i][1]=f[i];ll val=1;
for(int j=2;j<=n;j++)
{
val=val*i%mod;
g[i][j]=val*jc[i-1]%mod*inv[j]%mod*dp[i-1][j]%mod;
g[i][1]=(g[i][1]-g[i][j]+mod)%mod;
}
for(int x=1;x<i;x++) (dp[i][2]+=g[x+1][1]*inv[x]%mod*g[i-x+1][1]%mod*inv[i-x])%=mod;
for(int x=3;x<=i;x++) for(int y=1;y<i;y++) (dp[i][x]+=dp[i-y][x-1]*g[y+1][1]%mod*inv[y])%=mod;
}
memset(dp,0,sizeof(dp));dp[0][0]=1;
for(int i=2;i<=n;i+=2)
{
for(int j=2;j<=i;j+=2)
{
ll val=(j==2?1:(jc[j-1]*inv[2]%mod))*j%mod*C[i][j]%mod;
for(int p=1;2*p<=i;p++) (dp[i][p]+=dp[i-j][p-1]*val)%=mod;
}
for(int j=1;2*j<=i;j++) (h[i]+=dp[i][j]*g[j+1][1]%mod*inv[j])%=mod;
}
ll ans=n==2?1:(jc[n-1]*inv[2]%mod);
memset(dp,0,sizeof(dp));
for(int j=2;j<=n;j+=2) dp[0][j]=(j==2?1:(jc[j-1]*inv[2]%mod))*j%mod;
for(int i=1;2*i<=n;i++) for(int j=2;j<=n;j++) for(int p=2;p<j;p++) (dp[i][j]+=dp[i-1][j-p]*C[j-1][p]%mod*h[p])%=mod;
ll val=1;
for(int m=1;2*m<=n;m++)
{
(ans+=dp[m][n]*val%mod*inv[m])%=mod;
val=val*n%mod;
}
printf("%lld\n",ans);
return 0;
}
|


