一道很好的 dp 题。
题目链接。
题意
现在有 个城市与一个数字 。
个城市之间用若干条无向边连接。并且任意两座城市互相可达。
并且满足对于任意城市 ,都有城市 到城市
的距离严格小于城市 到城市 的距离。
求总共有多少中连边的方案,对数字 取模。 可能不是质数。
题解
首先考虑一下符合条件的连边方式有什么特性。
想想就会发现,我们只要将所有点按照到
的距离进行“分层”,就能得到很好的性质。
举 个例子:
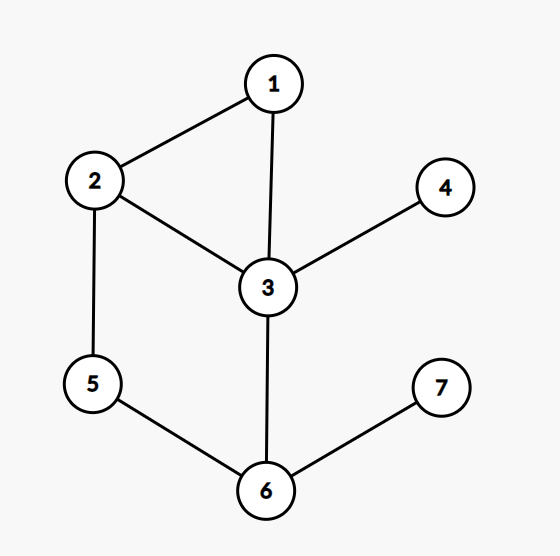
这张图符合条件,所有点到
的距离分别是 。
现在我们来分层。
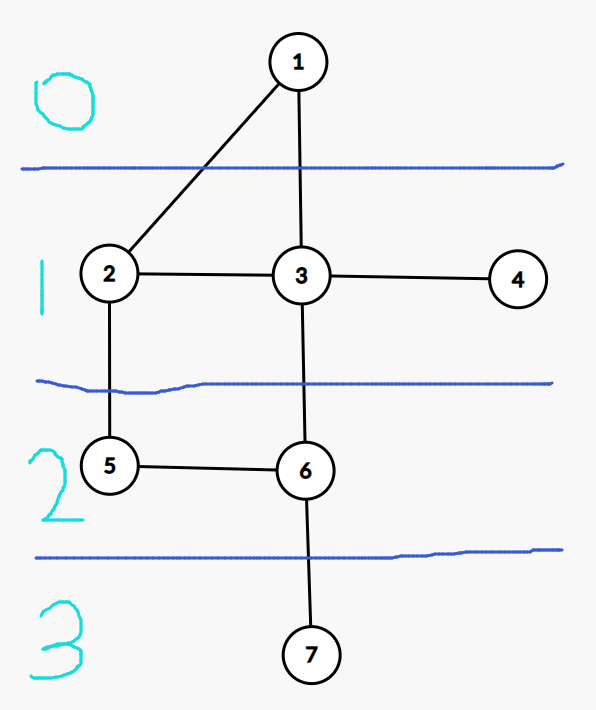
发现什么了吗?
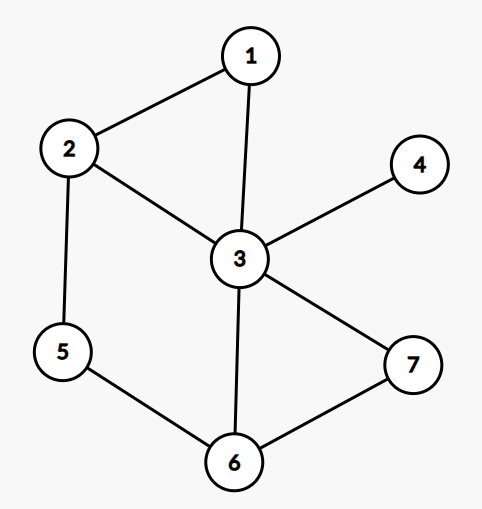
这场图不符合条件。所有点到
的距离分别是 。
现在我们来分层。
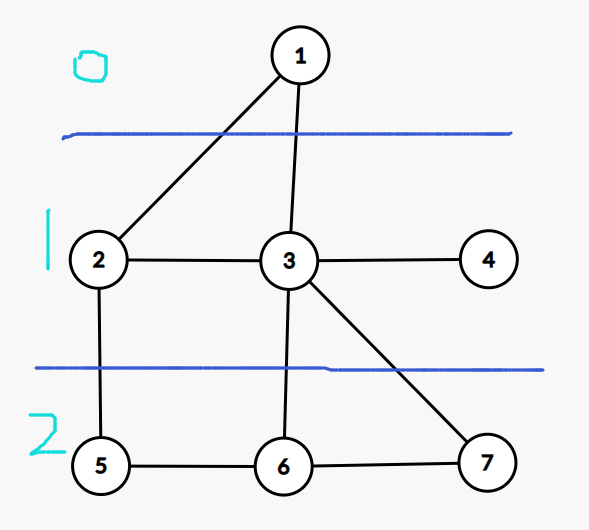
发现什么了吗?
我们可以发现满足条件的图都有这些性质:
- 点 在第 层;
- 点
在最后一层,并且最后一层只有点 ;
- 对于每一条边,两端的点所在层数只差不超过 (也就是说,只可能存在同层之间连边,或相邻两层连边)。
第
条性质可能不太显然,但推一下就会发现,不可能存在一条边,两端点分别在第
层且 。
因为如果这样的话,在第
层的那个点最多应该在
层,不可能在 层。
有了这几条性质,我们就可以直接进行 dp 了。
我们首先设 为 个点形成了若干层,最后一层有 个点的连边方案数。
那么就有 。
其中,枚举
为倒数第二层有多少个节点。
表示上一层有 个点,下一层有 个点,这两层之间连边方式有多少种。
可以知道 ,其中
是下一层其中一个点的方案数(每一个点至少与上一层连一条边)。
表示同层之间连边方案数,显然每一条边连不连都一样。
表示从剩下的所有点中,选出
个点,指定为当前最后一层的点。
因为点 和点 位置已经固定,所以看起来比较奇怪。
边界条件为 。
最后只需要根据
的值算出答案即可。
时间复杂度为 。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| #include<algorithm>
#include<cstring>
#include<cstdio>
#include<vector>
#include<queue>
#include<map>
#define inf 0x3f3f3f3f3f3f3f3fll
using namespace std;
using ll=long long;
using pli=pair<ll,int>;
using pi=pair<int,int>;
template<typename A>
using vc=vector<A>;
inline int read()
{
int s=0,w=1;char ch;
while((ch=getchar())>'9'||ch<'0') if(ch=='-') w=-1;
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
ll C[501][501];
ll dp[501][501];
ll sum[501][501];
ll p[250001];
ll jc[501];
ll inv[501];
int n,mod;
ll ans;
inline ll qow(ll a,int b)
{
ll ans=1;
while(b)
{
if(b&1) ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}
return ans;
}
inline void Add(ll &a,ll b)
{
a=(a+b)%mod;
}
int main()
{
n=read(),mod=read();
dp[1][1]=1;
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) sum[i][j]=qow(qow(2,j)-1,i);
jc[0]=p[0]=1;
for(int i=0;i<=n;i++)
{
if(i) jc[i]=jc[i-1]*i%mod;
C[i][0]=C[i][i]=1;
for(int j=1;j<i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
for(int i=1;i<=n*n;i++) p[i]=p[i-1]*2%mod;
for(int i=2;i<n;i++) for(int j=1;j<i;j++)
{
for(int k=1;k<=i-j;k++)
Add(dp[i][j],dp[i-j][k]*sum[j][k]%mod*C[n-1-(i-j)][j]%mod*p[j*(j-1)/2]);
}
for(int i=1;i<=n;i++) Add(ans,dp[n-1][i]*sum[1][i]);
printf("%lld\n",ans);
return 0;
}
|
感谢观看!



