Wuyanru's blog
0%

20250409 作业

发表于 分类于 ，

感觉这次的题单非常之牛啊！

CF1153F. Serval and Bonus Problem

题意

现在有一条长度为 的线段，然后在其上随机 条线段（随机的方式是随机两个实数点，然后左边的当作左端点，右边的当作右端点）。

再给定一个数字 ，求期望有多长的地方，至少被 条线段覆盖。

。

题解

应该算是套路题。

考虑这题的点是在实数域上随机，不妨假设没有任何两点坐标相同。

然后我们可以只考虑这 个点的相对顺序，显然相邻两个点之间长度期望为 。

设 表示现在有 个点，随便匹配的方案数是多少，显然有 和 。

考虑其中的第 条线段，其左边有 个点，右边有 个点，那么容易知道其覆盖次数 的概率为： 所有 条线段的概率加起来再乘 即可。

时间复杂度 。

提交记录。

CF1097F. Alex and a TV Show

题意

现在有 个初始为空的多重集和 次操作，每一个操作为以下 种之一。

  1. 令多重集 。
  2. 令 ，此处多重集的并为每一个数字出现次数相加。
  3. 令 ，其中 定义为 。
  4. 查询 中 的出现次数，输出其 的结果。

，，。

题解

对于一个可重集 ，设 表示 中数字 的出现次数。

首先考虑如何快速计算 ，容易发现这玩意看起来很像 FWT。

那么我们令 ， 同理，那么就会有 。

由于我们只需要维护出现次数 的值，那么考虑使用 bitset 维护正变换后的集合。

对于一操作，我们可以预处理出单个元素经过正变换之后长什么样子，然后直接赋值就 ok。

对于二操作，相当于两个集合出现次数直接相加，那么就是两个 bitset 异或一下。

对于三操作，就是两个 bitset 按位乘起来，相当于直接 and 一下。

对于四操作，也可以提前预处理每一个位置逆变换之后，和哪些位置有关，然后直接 and 一下再 count 一下就好了。

时间复杂度 。

提交记录。

CF1205E. Expected Value Again

题意

对于一个字符串 ，定义 为其真 border 的数量。

给定 ，求所有长度为 ，且字符集大小为 的串 的 的期望。

。

题解

不难发现，一个串有长为 的 border 等价于其有长度为 的循环节。

设 表示串 的循环节大小构成的集合，考虑组合意义： 那么考虑拆贡献，先看前半部分。

前半部分好算，相当于是对于每一个 ，我们要算有多少个串有长度为 的循环节，答案是 。

对于第二部分，相当于是需要计算对于 ，计算有多少个串同时有长度为 的循环节。

考虑将每一个位置看成一个点，对相同的位置进行连边，那么方案数相当于是 的连通块个数次方。

那么先把所有长度为 的边连上，现在形成了 个连通块，然后对于 ，给连通块 和 连一条边。

连的边里面，一定是恰好最前面 条边会合并连通块，那么答案为 。

也就是说我们需要计算 。

考虑枚举 和 ，现在我们需要计算合法的 的对数。

注意到一定有 ，所以这部分只有 对 。

设 ，则合法的对数为 。 直接枚举 ，时间复杂度是 的。

提交记录。

CF1292F. Nora's Toy Boxes

题意

现在有 个不同的数字 。

现在可以进行若干次操作，每一次选定三个不同的下标 满足 和 ，然后把 从序列中删掉。

求有多少种方案，删掉的数字最多。

两个方案相同当且仅当删除数字的顺序相同，与 无关。

。

题解

首先考虑最多可以删除多少个数字。

首先建一张图出来，如果 ，那么我们连一条有向边 ，由于没有相同的数字，所以这是一张 dag。

还是很难考虑最多可以删掉多少个数字，不妨倒过来考虑，我们计算初始最少可以有多少个数字，然后通过操作，添加数字，变成给定的集合。

首先连通块之间是独立的，所以我们不妨假设整张图连通，设 为点集。

设 为 中入度为 的点， 为 中入度 的点，那么显然 中所有点初始的时候必须存在。

对于 中的点，显然初始的时候要存在至少一个点（除非这个图只有一个孤立点）。

那么我们来证明，只要初始的时候 中至少有一个点，就可以将整个集合构造出来。

首先容易发现，对于 中的任何一个点，其至少有一条来自 的入边，否则其至少有一条来自 的入边，而整除满足传递性，矛盾。

那么将 中的集合分为 ，分别为当前存在／不存在的点集，若 ，我们考虑是否能加入一个新的点。

此时若存在一个点 ，且点 至少有一条向 的出边和一条向 的出边，我们就可以直接进行一次操作。

否则所有的 中的点都只和 中的点或 中的点有连边，则整张图不连通，矛盾。

这样我们就证明了此时一定能进行一次操作，所以只要初始的时候 中所有点和 中任意一个点存在，就能将整个集合构造出来。

这样我们就求出了最大的删除点的次数，我们还剩方案数需要求。

一个暴力的 dp 是这样的，设 表示初始的时候 有一个点，经过了若干次操作，现在 中存在的点有 这个集合，方案数是多少。

显然，这个东西复杂度很大，完全过不了。

考虑变一下状态，设 表示当前进行了若干次操作， 中的 这些点，出边里至少已经有一个点存在，且当前 ，方案数是多少。

这个玩意看起来就好离谱，但是他是可以转移并且算出答案的，考虑一下两种转移：

  1. 加入一个点 ，这个点的在 中的入边 满足 且 。

    显然我们知道，当前可以把 这个点加进去，并且显然 这个点之前并不存在。

    那么我们直接可以进行转移 。

  2. 加入一个点 ，这个点在 中的入边 满足 。

    如果这个点 之前不存在的话，显然我们可以通过一次操作将这个点加入集合，有转移 。

    但是问题在于，我们并没有记录当前有哪些点存在，我们无法判断 当前是否存在。

    这里就是这题喵的地方了，我们不考虑一个具体的点 能否被加入，我们考虑当前总共有多少个点可以被加入。

    由于我们现在知道 ，所以我们直接就能知道，当前有多少个点是下一次操作能直接加进去的，我们直接随便挑一个点转移即可。

考虑时间复杂度，为 ，但是 中的点没有倍数关系，并且所有点还得形成一个连通块，这个条件是相当严格的，所以应该跑的很快。

提交记录。

CF1085G. Beautiful Matrix

题意

我们称一个 的矩阵是好的，当且仅当其满足以下两个条件：

  1. 这个矩阵的每一行都构成了一个 的排列；
  2. 对于 ，有 。

给定一个好的矩阵，求有多少个好的矩阵字典序比他小。

。

题解

先考虑有没有什么复杂度稍微高一点的做法。

先枚举 表示两个矩阵第一个不同的位置，然后再枚举 ，考虑后续方案数。

方案数分为两部分，第一部分是第 行剩下的部分，第二部分是 行及以下的部分。

不难发现，第二部分直接就是错排，第一部分剩下的东西也是一个类似于错排的东西。

设 表示填一个长度为 的排列，其中前 个位置填的数不能与自己相同，方案数是多少。

这个感觉其实就是错排的 暴力，有转移 。

那么这样我们就得到了一个 的做法，其实 也是简单的。

  1. 若 ，则后面填的数字没有任何限制，答案直接是阶乘。

  2. 否则，设 为数字 在第 行的出现位置。

    若 填了数字 ，那么一共只有 和 两种情况。

    设 ，那么显然后续的方案数为 。

树状数组维护一下，就能做到 。

提交记录。

CF708E. Student's Camp

题意

现在有一个 网格，对于除去第一行和最后一行以外的每一行，每一天会发生如下的事情：

每一天早上，如果这一行还有至少一个格子，那么这一行的第一个格子有 的概率消失。

每一天晚上，如果这一行还有至少一个格子，那么这一行的最后一个格子有 的概率消失。

求 天之后，从第一行每一次走一个四联通格子，能走到最后一行的概率。

，。

题解

首先容易发现每一行剩余的部分是一段完整的区间。

其次我们可以知道，对于每一行来说，其左端点的位置和右端点的位置是独立的。

那么考虑如何进行计数，考虑对于一种合法的方案，我们将其对应到唯一的一条从第一行走到最后一行的路径上。

设计如下的策略：每一次能往下走就往下走，如果不能往下走就往左／往右走到第一个能往下走的位置然后往下走。

不难发现，一个合法的网格一定能够通过这个策略走出一条路径。

考虑这么一件事情，如果我们再某一行先往左走了一段距离，再往下走，说明了什么。

这说明，我们初始的位置，在下面一行已经被摧毁了，并且我们往下走的第一个位置恰好是下面一行的右端点。

那么我们就可以直接 dp 来计数了，设 表示我们现在从 往下走到了 这个格子。

第 行第 个格子没有特殊限制／需要是这一行左端点／需要是这一行右端点，概率是多少。

然后前缀和优化一下转移就好了，复杂度 。

提交记录。

QOJ8047. DFS Order 4

题意

定义如下的树是好的：

  1. 对于所有非根的节点，其父亲的编号比自己小；
  2. 一个点的所有儿子编号按照从小到大的顺序排序。

问对于所有有 个点的树，其总共会产生多少不同的 dfs 序，答案对输入给定的质数取模。

。

题解

首先考虑什么样的 dfs 序能被算进答案里面。

对于一个给定的 dfs 序，考虑逐渐往里加点，贪心构造一棵树。

假设当前整棵树向右的一条链是点 ，现在我们想要加入一个点 ：

  1. 若 ，则我们可以直接把 挂到 的儿子里面。

  2. 否则我们需要找到一个位置 ，然后把 挂到 的最后一个儿子。

    不难发现，这需要满足 ，因为 挂上去之后是 的后一个兄弟。

    容易说明，按照贪心，我们一定是找到这样一个最大的 ，然后把点 挂过去。

这样对于一个合法的 dfs 序，我们将其对应到了一棵树上去，而显然一棵树显然恰好有一个 dfs 序。

那么我们就可以对树进行计数，考虑根据上述的构造过程，什么样的树是合法的：

  1. 对于每一个非根节点，其标号比自己的父亲标号大。
  2. 对于一个点的所有儿子 ，满足：
    1. ；
    2. 对于 ，点 至少有一个儿子；
    3. 对于 ，点 的最后一个儿子标号 。

我们现在需要对满足这样条件的树来计数。

我们不妨把这个限制画出来，其中一条边 表示点 的标号比 小。

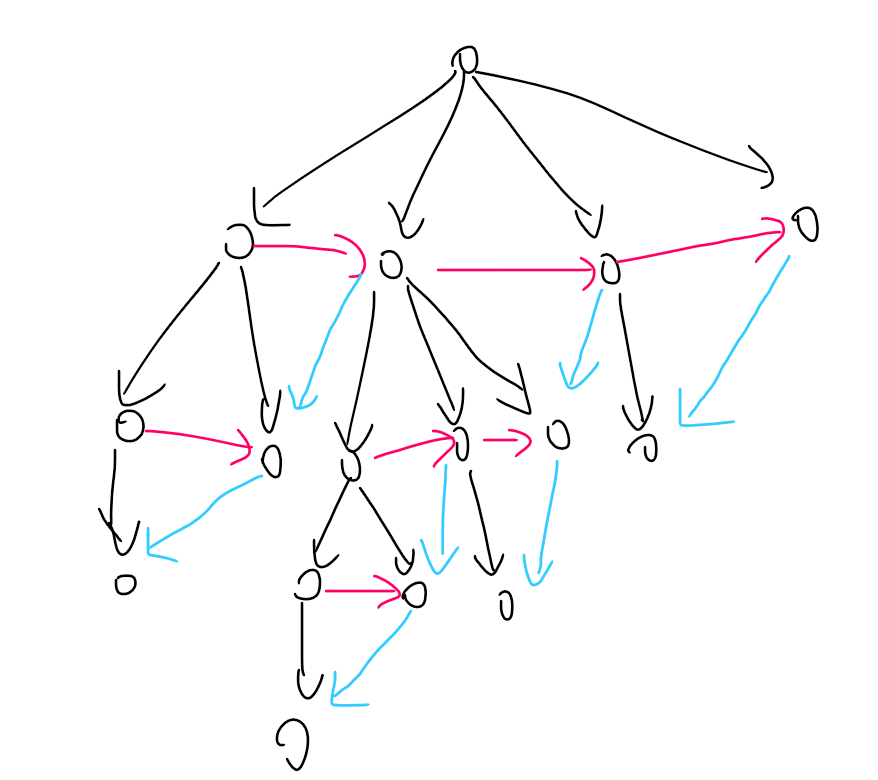
这样不好计数，我们不妨先回忆，假设所有连边形成了一个外向树，方案数怎么算。

可以发现，答案是 ，那么上面这棵树怎么记方案数呢。

我们将所有的蓝色边反转，然后删掉无用的边，发现原来的连边变成了一条链。

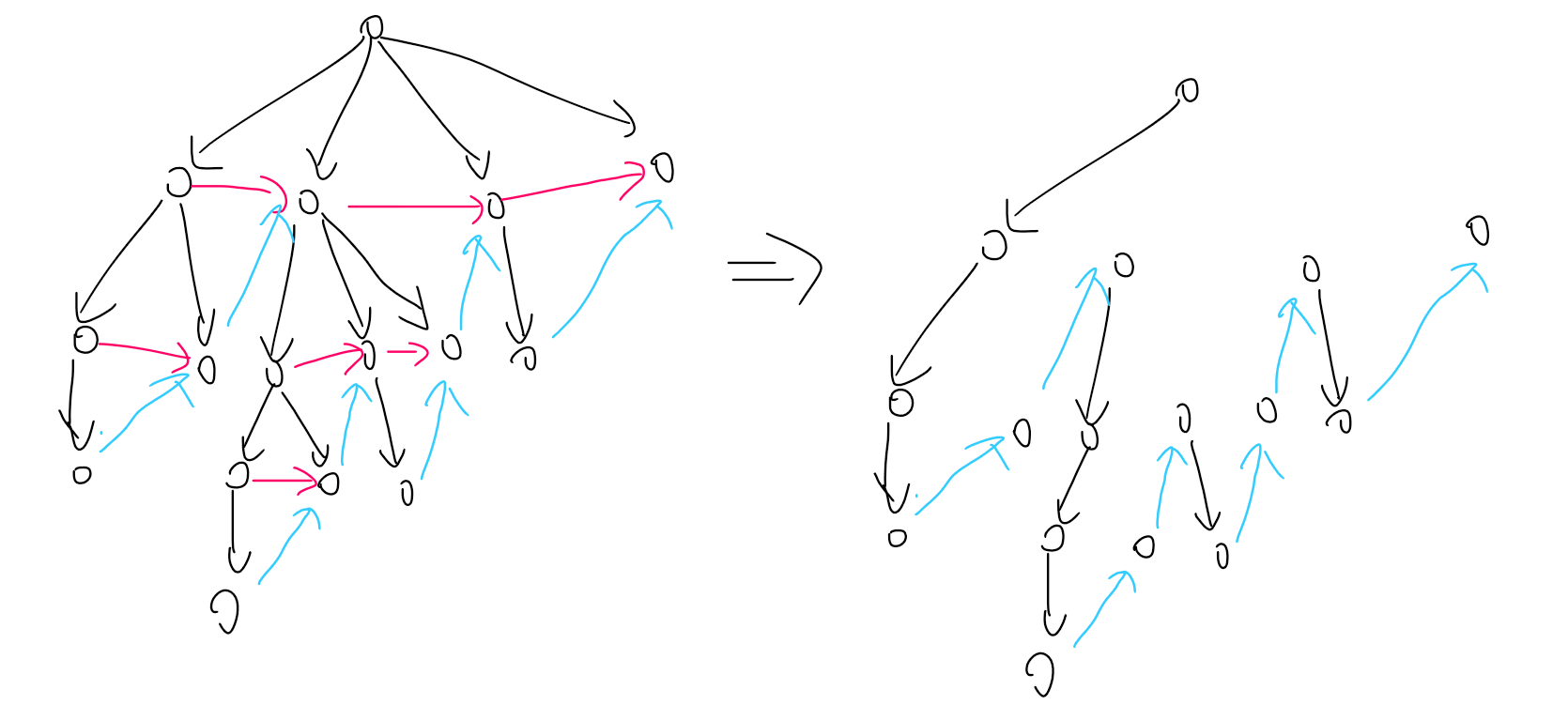
我们考虑对蓝边进行容斥，即删掉一些蓝色边，并且把剩下的蓝色边反转。

多玩几组就会发现，剩下的有用边总是一棵外向树，这说明我们的做法非常有前途！

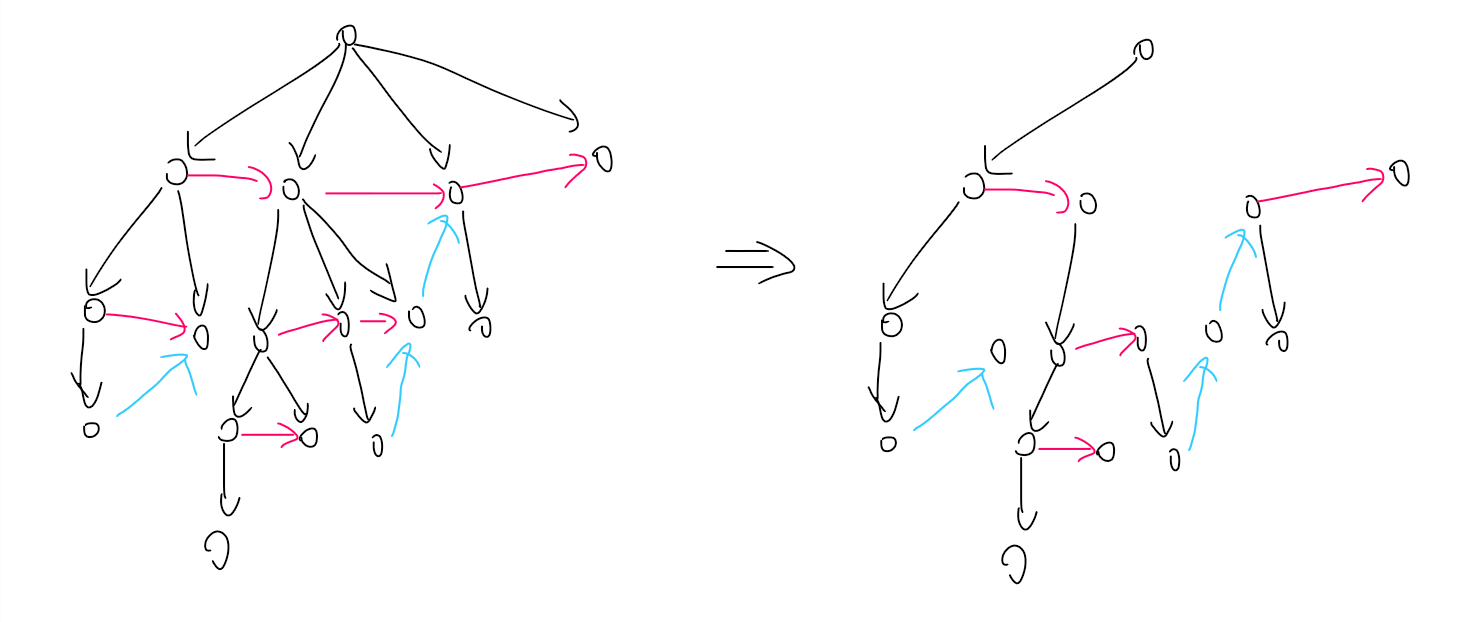
考虑如果已经确定了每一条蓝色边是反向还是删掉，这棵外向树会长成什么样子。

假设现在点 的两个相邻的儿子 ，其中 的最后一个儿子 。

首先无论如何，因为初始 这条路径的存在， 一定不在最终的那棵树上。

那么考虑原先 这条蓝色边，如果这条边反向了，那么 的红色边没有用。

这个时候整个 这棵子树被挂在了 下面。

如果 这条蓝色边整个被删掉了，那么 仍然保留， 整棵子树会被挂在 上。

（当然这种关系是可以嵌套的，例如上面那个图里面，连着两个反向边，导致旁边的子树挂在了奇怪的地方）

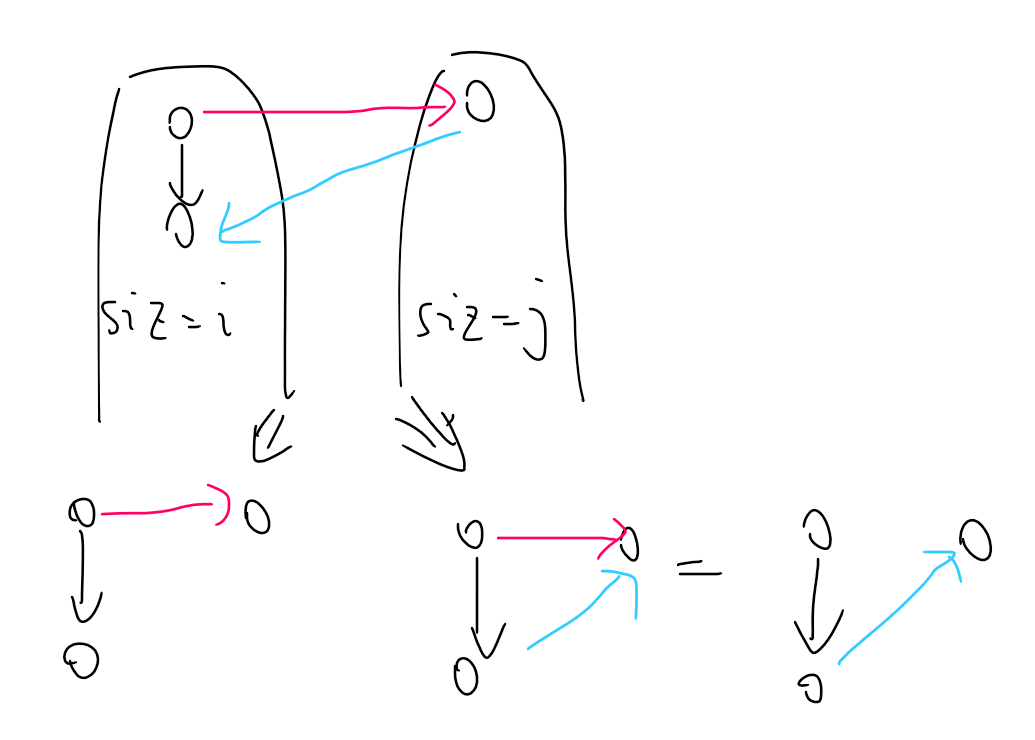
那么考虑 dp，设 表示大小为 的子树，子树右边必须接一个大小为 的形态已确定的子树，所有方案的 和是多少。

转移的话考虑令 表示若干棵子树连成兄弟， 之和为 ，并且右边连一个大小为 的子树，权值之和。

容易从 转移过来， 的话直接枚举第一个子树的大小即可。

时间复杂度 。

提交记录。