Wuyanru's blog
0%

[差 5 题] 20250317 部分作业

发表于 分类于 ，

你说的对但是我只是想记一下这一天讲了哪些题然后慢慢看题解。

感觉一天讲的题我一周都写不完。

ARC193D. Magnets

题意

给定两个长为 的 串 。现在有 个单元格，其中第 个单元格上有 个石子。

现在可以进行若干次操作，每一次操作选择一个格子 ，然后所有石子会向第 个格子移动一格。

目标是让第 个格子上有石子当且仅当 。问最少操作次数。

。

题解

首先假设我们不能对第一个石子或最后一个石子所在的位置进行操作，这个题应该怎么做。

考虑如果我们的操作位置在第一个石子左边，则所有石子都会向左移动一格；在最后一个石子右边同理。

如果是在第一个石子和最后一个石子中间，则左边一部分石头会往右走，右边一部分往左走，最左侧和最右侧的石子距离会减少 。

那么这样我们就直接能算出在中间应该操作多少次，那么在两边操作的次数也能算出来了。

也就是说，我们直接能把答案算出来，唯一需要干的事情是判是否存在合法的操作方案。

首先可以发现，一定是 中的连续一段石子对应 中的一个石子。

那么考虑如何判断一个对应的方案是否是合法的。

既然已经确定了方案，那么我们现在能确定 中的相邻两个石子，在操作结束的时候，距离应当是多少。

因为我们知道两个石子间的距离是只会减少不会增加的，所以如果出现了结束距离比现在的距离还大的情况，一定是不合法的。

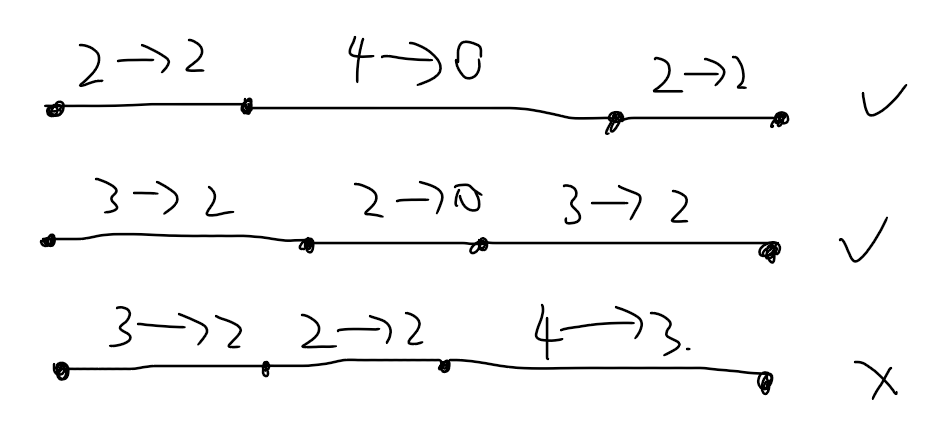
即使满足了这个条件，也有可能是不合法的，例如这张图的第三种情况。

为什么呢，因为我们如果对中间的某一段进行一次操作，他的长度会减少 。

如果前后长度奇偶性相同的话，我们只操作段的中间就可以达成目标。

但如果奇偶性不同的话，就需要操作石子的位置，这样会使前后两端的长度各减少 。

但如果出现上面的第三种情况，就会出现把左侧或者右侧段搞爆的情况。

所以此时还有另外的一个条件，就是如果某一段的起始长度和目标长度一样，需要满足左右两侧的奇偶性相同。

不难发现，满足了这两个条件，方案就一定是合法的。

这样的话我们直接贪心就行了，这样就解决了，不允许在第一个和最后一个石子处操作的情况。

那么考虑现在我们可以在这两个位置进行操作，不难发现，如果我们在第一个石子（假设为 ）处操作了两次。

那么我们可以改成先操作一次 ，再操作一次 。

这有什么用呢，我们发现，如果存在合法操作，那么其中肯定存在一种，满足第一个石子和最后一个石子各被最多操作 次。

那么我们直接枚举第一个和最后一个石子有没有被操作过就好了。

时间复杂度 。

提交记录。

CF2077F. AND x OR

题意

对于两个长度均为 的数组 ，若能通过执行若干次如下操作，使得 ，则称有序对 是好的。

操作为选定两个不同的位置 和一个数字 ，并令 ，。

给定两个长度为 的值域在 的数组 ，现在可以花 的代价给 或 的某个位置加上 。

问最小代价使得 是好的。

。

题解

先来考虑什么样的数组对是好的，首先如果这两个数组长得完全一样，那么一定是好的。

否则，一定进行了至少一次操作，那么一定存在一个 满足 。

不难发现，只要存在这样的 ， 就一定是好的。

从构造的角度证明，首先先把出了 以外的位置全部弄对，只是好做的。

然后可以通过选取 让 。

首先令 ，，则 ，。

然后令 ，，则 ，，构造完成。

那么我们找出了 是好的的条件，考虑这道题怎么做呢。

首先算出来操作完之后 相等的情况，对于剩下的情况，显然只会对 进行操作。

我们现在的目标是操作完之后存在两个不同的位置 满足 。

考虑枚举 和 ，其中 ，首先判掉 的情况。

考虑我们现在要选出两个数字满足 和 ，最小化 ，但是 标号不能相同。

设 ，那么若 ，则选出的 一定是不优的，因为此时一定有 ，把 变成 显然代价更小。

所以我们相当于对于所有 和 求 的最小值。

那么考虑对于每一个 维护其子集内最小和次小的 ，满足最小和次小的 不同。

这样直接算就好了，时间复杂度 。

提交记录。

CF2077G. RGB Walking

题意

给定一张有 个点 条边的无向图连通，每一条边有一个边权和一个颜色（RGB 之一）。

保证每一种颜色的边都至少有一条。

对于从 到 的路径，设 为路径上所有红色边的边权和， 同理。

求出所有路径的 的最小值。

。

题解

考虑如果原图中恰好只有一条从 到 的路径，这题该怎么做。

由于一条边可以走任意多次，所以考虑通过重复走一条边来令极差最小。

这就很有一种三元一次不定方程的感觉了，考虑令 表示颜色 所有边权的 ， 表示所有 色的边权和。

那我们一开始提前把颜色为 边走上 遍，这样我们仍然在点 ，并且此时三种颜色边权和相等。

这样就可以看成可以可以任意增减一条边的经过次数（最小单位是增加或减少 次）。

考虑对于一条路径来说， 显然只可能有 和 两种取值。而当整张图只有一条路径的时候，这个取值是固定的。

也就是说现在有方程 ，其中 为定值，我们需要选取合适的 使得 的极差最小。

考虑只有两种颜色 的话怎么做，不妨假设 ，那么直接做一个类似 excrt 的东西就好了。

三种颜色的话同样先假设 ，然后枚举 的值，然后就变成两种颜色的情况了。

这样我们就解决掉了原图中只有一条从 到 路径的情况。

考虑一张普通的图，其实做法差不多，我们还是先选一条 开头和结尾的路径，使得每一条边都走了很多遍。

这是容易的，可以直接构造一个欧拉回路得到。

唯一和上面不同的是，我们现在无法确定 到底是取 还是 。

由于只有两种取值，我们直接 bfs，对于每一个 算出是否存在以 开头 结尾的路径，使得 分别是 。

后面是一样的，时间复杂度 。

提交记录。

还没写的题

CF2079A

CF2080A

CF2068B

CF2068G

CF2068I