20250209 部分作业

题好难，不嘻嘻（2）。

只保留了我认为比较有意义的题（2）。

我怎么感觉所有题最后都会保留。

CF1707E Replace

题意

给定一个长度为 的数列，第 个数为 ，满足 。

定义 ，和 。

给定 组询问，第 组询问给出 ，求出最小的 满足 。

。

题解

为啥这 3500 的题一个白天就过了快 40 个人。

首先可以知道一个结论是 。

这个比较显然，因为容易证明得到的两个区间左右端点一样，并且中间肯定是连续的。

然后还有 。

这个容易归纳证明，首先 。

然后假设 的 全部都已经证明了，现在需要证的相当于 。

那么一定 ，那么 和 。

所以显然 。

那么这个时候就会发现 。

一样，左右端点归纳一下，然后中间还是连续的，所以是相当的。

那么现在考虑我们怎么样回答答案。

首先如果 且 ，那么直接特判掉。

否则如果不存在 或者不存在 那么肯定无解。

否则一定会有 ，这是有单调性的，我们可以倍增！

考虑能不能维护出来 。

假设我们知道 ，那么 的左端点就是 。

那么我们直接倍增再套一个 st 表就对了。时间复杂度 。

提交记录。

CF1852F Panda Meetups

题意

现在有一个数轴和 个操作，操作共有以下两种：

1. 时刻在 这个位置插入 个红点。

   每一个红点在每一个时刻可以选择往左走一步、原地不动或向右走一步。

2. 时刻在 这个位置插入 个蓝点，蓝点下一个时刻就会消失。

   但是如果在 时刻 上面有 个红点，那他们会造成 对匹配，匹配的点会消失。

对于每一个操作的前缀，求出最大的匹配个数。

保证操作按照 不降的顺序给出。

。

题解

先考虑静态的区间怎么做，考虑把蓝点和红点画在一个平面上。

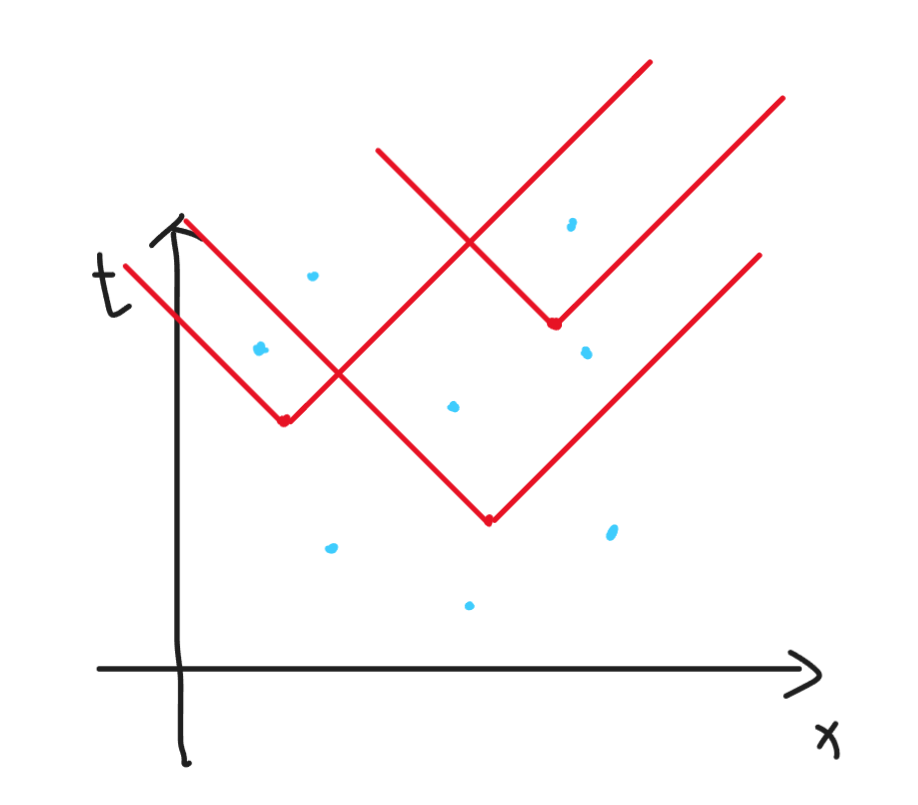
一个红点可以匹配它上方的蓝点，所以这可以看作一个匹配问题。

直接跑网络流显然不太可能，所以我们考虑求出这张图的最大独立集。

也就是说，我们要尽可能选出更多的蓝点和红点，使得没有任意一堆点可以匹配。

那么就能发现，一定存在一条分割线，使得线上面的所有红点都被选中，线下面的所有蓝点都被选中。

并且这条边在 相邻的两个位置，差的绝对值不超过 。

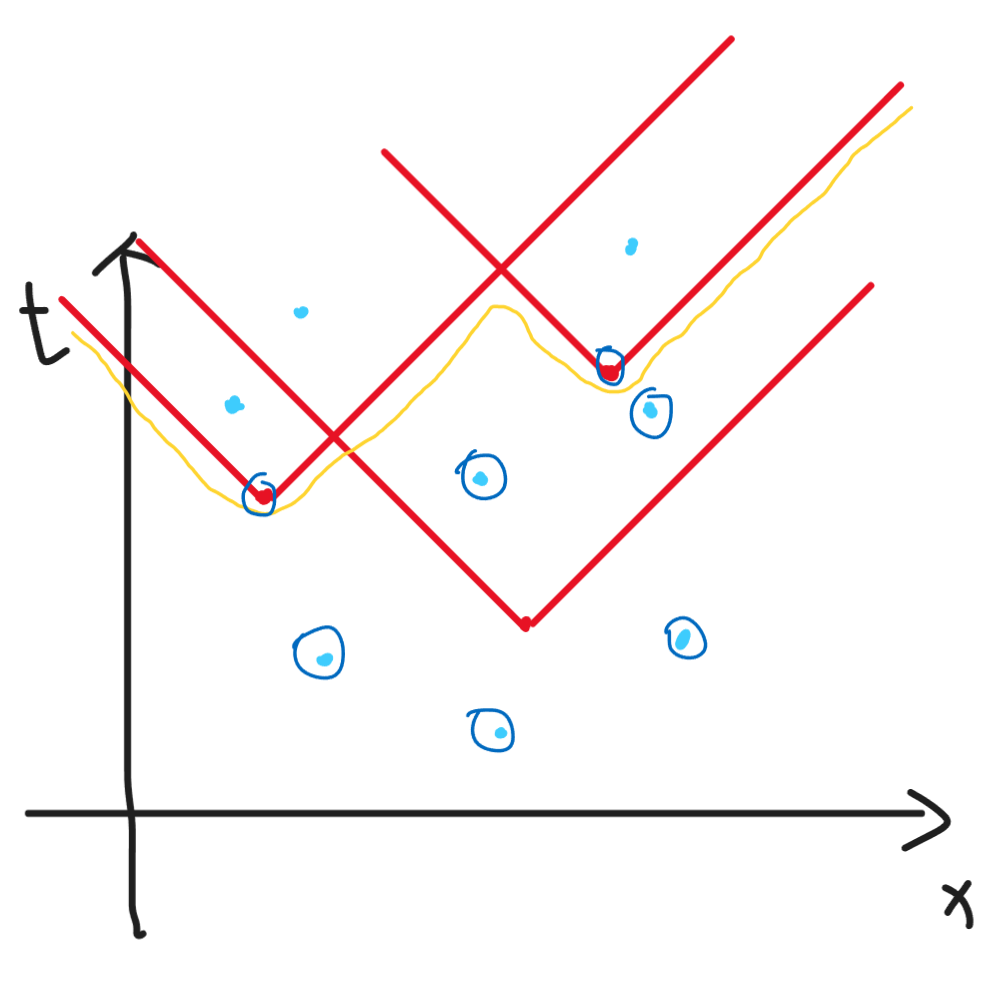
由于每一次加点 是不降的，那么考虑直接从左往右扫。

那么直接令 表示扫到 的位置，现在折线的高度是 ，那么操作分为两种。

第一种操作是把 dp 往后转移一个位置，那么 。

第二种操作是遇到一个点，直接给一段前缀或者一段后缀整体 。

那么我们考虑维护 的差分即维护 ，使用平衡树维护 不为 的位置。

考虑如果扫到位置往后挪了一个，那么差分为正的位置会往左走，为负的位置会往右走。

由于一负一正相撞之后会抵消一部分，所以还需要维护最近的两个一负一正的位置。

时间复杂度 。感觉有点过于难写了。

提交记录。

CF1523H Hopping Around the Array

题意

现在有 个点，每一个点有一个权值 ，表示如果现在在 点，则可以跳到 中的任意一个点。

给定 组询问，每一次给定 ，询问现在在 ，你在跳之前可以选择 个点删掉，跳到 至少需要多少步。

，。

题解

考虑 的时候怎么做。

可以发现，（除了最后一步以外）我们每一次跳到的点，一定是能跳到的，满足 最大的点 。

那么就可以直接 表示从 这个点开始跳，跳 次会到哪一个点。

询问的时候就直接算出跳多少步能跳到一个 的点 ，然后再跳一步就是答案。

那么现在考虑 ，显然直接改一下就好了。

设 表示从点 开始跳 步，这 步以内最多可以删 个点，最远可以跳到哪里。

询问的时候处理方式相同，时间复杂度 。

提交记录。

CF1824E LuoTianyi and Cartridge

题意

给定一棵树 ，每一个点有点权 ，每一条边有边权 。

现在你需要建一棵新树 ，首先任意选择一个点集 ，然后重复下面这个过程 遍

选择一条 中的边 ，与两个 中的点 。

要求 这条边之前没有选过，并且 在 中不连通，且 中 在 这条路径上。

然后将这条边加入 中，边权即为 。

令最后建出的 中， 最小值分别为 ， 的和分别为 ，最大化 。

。

题解

先来考虑，假设已经给定了选择的点集与边集，怎么判断能否连出一棵合法的树。

考虑对于任何一个不在边集内的边，我们把他的两个顶点缩起来。

这样可以得到一棵新的树，满足树上的所有边都在边集以内。

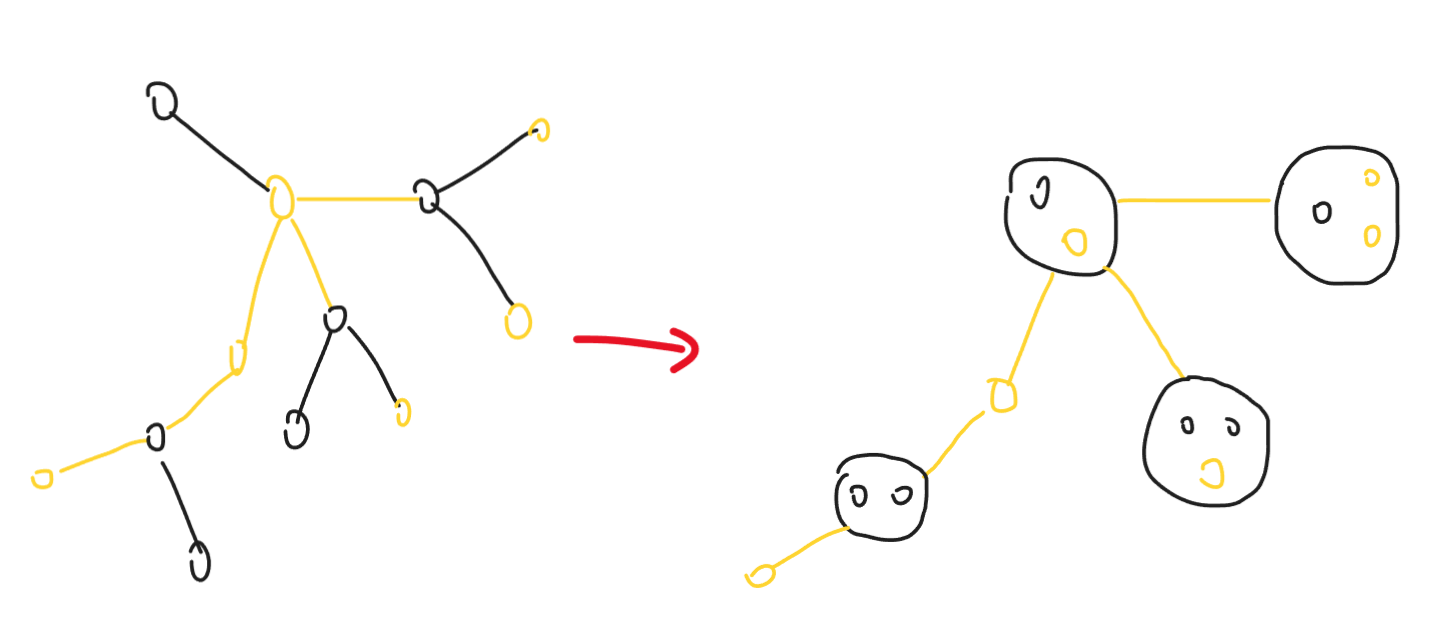
（其中黄色的为选中的边集或点集）。

可以发现，如果存在某一个叶子，满足其中没有黄色点，那么一定是连不出来的。

否则一定可以连出来，构造的方式是，每一次考虑一条还没有被用过的边。

此时所有点一定被分为 个连通块，并且这条边的左右两侧都有点集内的点。

那么一定能从左边选出一个连通块，然后从右边选出一个不同的连通块，然后把这两个连通块连起来就好了。

这样我们就会判断一个方案是否合法了。

那么考虑原题怎么做呢，首先答案中出现了 这样一个系数，说明我们肯定是得枚举 的。

枚举了之后，原树上有一些边和点是能选的，那我们还是一样把不能选的边都缩起来。

那么现在问题在于如何取点和边。

首先，对于某侧没有叶子的可选边，他实际上和不可选没什么区别，我们把他删掉（这样点集的叶子更好定义一些）。

然后，对于所有叶子，其内部必然要选至少一个点（否则与他相连的边就选不成了）。

所以每一个叶子中，可选的点里面 最大的点肯定要被选。

那么这样，我们的边集无论选成什么样子，就都是合法的了，所以在剩下的点和边里面都直接挑权值大的挨个选就好了。

那么这样就能做到 了，考虑优化它。

我们从小到大枚举 。

删掉一条边的时候，相当于合并其左右的两个点，我们使用启发式合并给这两个点并一下（需要注意两个点会变成叶子之类的问题）。

删掉一个点就是直接删了（大雾），同时也要注意此时可能连带删掉一个边，然后让别的点变成叶子。

可能还需要两个线段树之类的东西维护点权和边权的前 大值之和。

时间复杂度 。

提交记录。

CF2018E Complex Segments

题意

给定 个区间，第 个区间为 。

现在要选出若干个区间，并将它们分为若干组，满足：

1. 两个区间有交当且仅当他们被分在了同一组；
2. 每一组的区间个数相等。

求出选出的线段个数最大值。

。

题解

这题看上去就不太能直接做，所以考虑暴力一点的方法，先枚举 表示一组中有多少线段。

设答案为 ，那么 显然可以通过贪心来求出。

具体来说，考虑第一组怎么选，容易发现在合法的前提下，右端点的最大值肯定是越小越好。

那么我们将所有线段按照右端点进行排序，每一次假如一条线段，如果加入之后存在一个位置被覆盖了 次，那么第一组就可以直接结束了。

第一组结束之后，假设第一组右端点最大值是 ，那么我们忽略掉所有 的线段 ，继续去做第二组。

这样我们就能求出如果一组有 个线段，最多的分的组数。使用线段树优化可以做到 。

其实这个部分还能优化，假设有两个位置 ，满足在加入某条线段之后， 的覆盖次数大于 。

那么可以发现， 就废了，因为线段右端点是递增的，后面能覆盖到 的部分肯定可以覆盖到 。

也就是说，我们其实只需要维护覆盖次数为后缀 的位置。

那么直接使用一个链表，把所有最大值的位置串起来，并且维护他比前面一个后缀最大值小了多少。

假设现在新来了一条线段 ，那么我们首先需要找到 的第一个后缀最大值 ，然后链表上改一改就好了。

那么问题在于如何找到 的位置呢，容易发现，一个点如果某个时刻不是后缀最大值了，那么他之后就永远不会是后缀最大值了。

那就再用并查集维护每一个点后面的第一个后缀最大值位置，当某个点不是后缀最大值了的时候，把他并到他后面那个点上就好了。

忽略并查集复杂度的话，这样我们就可以在 复杂度内求出 。得到了一个 的做法。

考虑到 有非常好的性质，比如 和 。

那么我们使用分治来进行优化，考虑假设我们现在分治到了一个区间 ，并且我们知道 和 。

如果此时 ，那么显然区间所有位置的 都一样，可以直接退出。

否则我们计算出 ，然后分成左右两半进行递归。

因为 所以可以证明我们只会进行 次查询 的操作。

时间复杂度 。

感觉是最好写的一个题

提交记录。

CF1876G Clubstep

题意

给定一个长度为 的序列，第 个元素为 。

现在可以进行若干种操作，第 种操作是花费 的代价，给 增加 ，并且给所有 增加 。

次询问，第 次给定 ，表示询问如果要让所有 都有 ，最小代价是多少。

。

题解

考虑单组询问怎么做，容易发现直接从后往前贪就对了。

具体来说，找到最后一个满足 的位置 ，然后一直执行第 种操作即可。

那么可以发现，设 表示一个询问的答案，那么会有： 那么我们考虑拿一个平衡树从右往左扫，类似于那个插入标记回收的题（虽然我还没写。

大概就是扫到 的时候把询问插进来，然后扫到 的时候就能知道答案，问题在于扫过一个位置的时候怎么更新答案。

暴力的方法是对于平衡树的一段 的后缀，每一个节点都暴力更新一下，这显然寄了。

但是不难发现，在扫过几个位置之后，不同 的差距将会很快减小。

那么我们合并 相同的连续段，假设平衡树上第 个连续段 。

那么定义势能函数 。

那么考虑，如果 ，那么扫过这两个位置之后势能一定会减少 。

如果 ，那么势能可能不变也可能减少，如果有一堆这样的情况连在一起，那么至少会有一半的位置势能会减少。

也就是说，我们没多扫过一个位置，势能会减少大概 。

所以合并相同的 之后，复杂度是 的。

提交记录。

QOJ9918 Master of Both VI

题意

现在有 个点构成了一棵树，每一个点上面有一个怪物。还有 次操作，分为以下两种：

1. 给定 ，给 这条路径上的所有怪物施加 的伤害。

2. 已知点 上有一只血量为 的怪物，已知他现在血量 ，但你不知道他是什么时候出现在这个点上的。

   你需要求出，这只怪物最多接受了多少次攻击。

   特殊的，在怪物遭遇攻击的时候，可以使用技能，使自己收到的伤害减半（实数）。

   但是，怪物不能在相邻两次攻击中，都使用技能。

，。

题解

首先给所有伤害和血量 ，这样就不用实数了。

先来考虑，一个暴力一点的做法。

我们首先暴力维护出每一个点按照时间顺序依次受到了哪些攻击。

然后对于一个询问，假设这个点目前一共受到了 次攻击。

那么做一个 dp，其中 表示第 次攻击有/没有使用技能的情况下，承受 这些攻击最少会掉多少血量。

这样复杂度是 的。

假设第 次攻击的伤害是 ，那么可以发现： 那么相当于是： 可以发现这样就写成了一个 矩阵乘法的形式。

也就是说这个 dp 的过程可以使用线段树来优化。

我们以时间为轴，建一棵线段树出来，那么一组询问相当于是确定了一个右端点，要求我们找出一个最小的左端点。

这样 就能做到 的复杂度了。问题在于怎么对于不同点求出这个线段树。

假设所有攻击都满足 ，那么一个点的线段树之和它的子树内部有关系，这启发我们使用线段树合并来维护。

那么考虑直接在 处插入一个矩阵， 处插入一个矩阵，跑线段树合并，然后在 跑完之后给删掉就好了。

时间复杂度 。

提交记录。

CF1515H Phoenix and Bits

题意

给定 个数字，第 个数字是 ，还有 次操作，操作有两种：

1. 将 的所有 变为 。
2. 查询 有多少不同的 。

注意上面的操作是对值域而不是下标。

，，。

题解

首先考虑还是得用 trie，区间操作的话就先 split 出来然后再 merge。

然后查询查的是有多少不同的数字，所以如果有需要合并的地方，一定要立刻合并。

那么对于每一个点维护，其子树内，哪些层，出现了点，同时有两个儿子。

然后直接 dfs 下去，需要合并的就直接合并，剩下的打一个 tag 就解决了。

tag 可以使用位运算 下传，同时有儿子的信息也一样。

时间复杂度 。

提交记录。

QOJ9559 The Tower

题意

现在有一个弹幕网站，初始的时候所有行都是空的，按照时间发生了 件事，有以下几种：

1. 新来了一个用户发了 条弹幕，他会占用此时最上面的 个空行；
2. 一个用户跑路了，他占用的行会变成空行；
3. 查询某个行现在被哪个用户占用。

。

题解

先不考虑询问问什么，考虑怎么维护前两个操作。

可以发现，这个比较容易用线段树分裂求出来。

问题在于，询问的时候我们需要知道某个节点在哪一棵树里面，这不是很好做。

一个想法是，我们维护一下，线段树上面每一个叶子，分别在哪颗树里面。

然后 set 维护一下，这样就是两个 的做法了，但是这个 set 似乎不能用 unordered_map 之类的东西代替。

那我们考虑，再开一个线段树，这棵线段树记录的是，每一个区间，在那边的线段树森林里面，节点编号是多少。

这样对于询问，我们只需要在新开的这棵线段树上面从上往下找就好了，然后找到对应的节点之后，再从下往上跳。

提交记录。

CF1942H Farmer John's Favorite Intern

题意

现在有一棵 个点的树，每一个节点有一个权值 ，初始为 。

定义一次在 的生长操作为选择 的父亲或者 子树内的节点 ，令 。

定义一次在 的收获操作为选择一个 子树内的节点 ，令 。

给定 次操作，一个操作形如对点 重复 次生长／收获操作。

你需要对于操作的每一个前缀，求出，是否能够重排操作，使得过程中所有 非负，并且最后有 。

。

题解

因为操作可以重排，所以过程中 非负这个条件相当于没有，只要把所有生长放到收获前面就好了。

那么先来考虑，对于整体怎么判断是否有解。

考虑一个在 的生长操作，可以匹配一个 子树内或 的 。

也可以匹配一个在 子树内或 祖先的收获操作。

那么考虑从下往上贪心，一个点的生长操作，应当优先匹配自己子树内的东西。

然后优先匹配父亲的 ，其次是祖先的收获操作。

那么直接维护 ，分别表示 子树内需要多少生长，能提供给父亲的 生长有 个，能贡献给祖先的收获操作有 个。

这样我们就会算单个前缀答案。

我们写一个暴力发现没有问题

懒得写了之后再说