too hard for me!(2)
感觉其实是把官方题解翻译成中文之后加了点东西。
QOJ9875. Don't Detect Cycle
题意
给定一张
现在你需要按照顺序加入这
判断有没有解,有解的话还需要构造方案。
题解
正着不好做,考虑倒着做。
初始有一张图,需要找到一个删边的顺序,使得删完边之后的两个点不在一个环里面。
删完一条边的时候显然限制是会变弱的,所以这个时候一定是能删的尽早删。
那么求出这张图的边双,割边放到最后删肯定不劣,那么只需要考虑一个边双内部怎么办。
可以发现,一条边
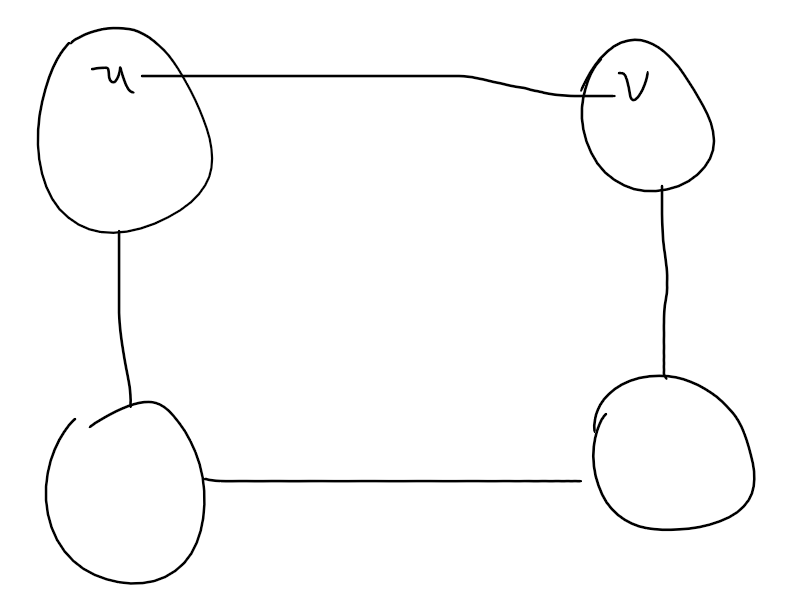
考虑
如果
所以
所以直接一条一条删就做完了。复杂度
提交记录。
QOJ9876. Self Checkout
题意
给定一个由
现在需要计算只包含
- 初始有一个空序列
。 - 若
当前不为空,令变量 ,否则过程结束,返回序列 。 - 若当前
中至少有一个 ,令 ,然后将序列中第一个 删掉。 - 若当前
不为空,将 加上序列第一个数字,然后将第一个数字删掉。 - 将
放到 的末尾,然后返回第二步
题解
首先考虑操作
枚举操作
那么
先来考虑前面的部分,先来考虑
然后考虑
然后考虑
只有可能最后一段是全
然后是操作
也就是说,
那么就只需要管前面即可。
提交记录。
QOJ9877. Segment Tree
题意
现在有一张
边有边权,所有边形成一个线段树的样子。
现在需要进行
题解
其实这道题相当于是,有一棵维护了区间和的线段树,每一次可以花费若干代价,询问线段树的一个区间和。
一个询问相当于给你一个区间,查询区间和,最少需要多少代价。
查询有几种方式:
- 如果查询的区间恰好对应了线段树上一个完整的点,那么可以直接查询这个区间;
- 将这个区间分成两部分,分别进行查询;
- 查询这个区间的某个超集,然后再查询超集减掉额外部分。
考虑如何计算代价。
首先,如果一条边的边权比他两个儿子的和还要大,那么我们先给他取一个
这样的话,方式
对于询问,考虑从其中一个点在线段树上一直往上跳,并维护其到每一个祖先的最短路。
另一个点同样处理,两个距离加起来取 min。
提交记录。
QOJ9879. ReTravel
题意
初始有一个机器人在原点。给定
操作共有以下
- 让机器人向
轴正方向走一步,将一个字符 添加到 末尾,花费 的代价; - 让机器人向
轴正方向走一步,将一个字符 添加到 末尾,花费 的代价; - 撤销
最后一个字符对应的操作,不花费代价。
题解
设
设
首先边界状态是
考虑当
假设此时第一个进行的操作为一操作,那么此时会先解决掉
此时一定不会有
此时也一定不会有
那么我们枚举
时间复杂度
提交记录。
QOJ9880. Origami Warp
题意
现在有
保证第一条直线为
现在有一个点
称点
给定
数据组数
题解
首先这个可达性有一些性质。
性质
:点 可以到达自己。
废话。
性质
:若点 能到达点 ,则点 能到达点 。
证明:若
那么把整个操作步骤倒过来,就能让
性质
:若点 能到达点 ,点 能到达点 ,则点 能到达点 。
证明:若
不妨设现在有两条直线,这两条直线的交点为原点
假设当前有一个点
那么我们首先可以知道,如果只使用这两条直线,则
考虑把点
再把点
画出一个以
此时,若
考虑题目的直线是以两个整数点的形式给出的,那么
在这个条件下,可以发现,若
那么,若两条直线的夹角不为
这样一个好的交点,就可以让我们把一个点移动到一个圆上的任何一个点去。
那么初始的时候,若至少存在一个好的交点,则说明存在至少一条直线,倾斜角不是
考虑此时若存在不为原点的好的交点,则平面上任意两点都可以到达。
否则,平面上只有原点一个好的交点,此时一个点可以到达所有和原点距离相同的点。
那么问题在于,如果此时没有好的交点,如何判断答案。
此时只会有倾斜角为
先来考虑一个一维的问题,现在有一个数轴,数轴上有
初始时有一个点
现在问能不能把点
那么
证明的话和上面某部分差不多,考虑把
后面就比较容易能证出来恰好是那两种情况能走过去。
有趣的事情是,如果我们将这
那么回到原题,此时若没有
再来考虑有
假设现在有三条直线交于一个点
为什么呢,假设一个点
那么按照
所以删除这条
那么也就是说三条直线里面,他们的效果有
初始的时候我们至少有一条
根据上面一维问题的相关证明,我们可以假设此时
那么我们现在至少有一条
(将
设
特殊的,还可以发现我们任意加一条
为什么呢,因为你可以看成把所有
此时,如果我们有两个
那么现在,我们拥有所有
此时有一种神奇的判断方式,考虑先枚举
然后后面的过程中,只使用
首先,这样能操作到的点,肯定是正常情况下能操作的。
我们现在需要证明,所有可达的点,都能通过这种方式操作得到。
考虑,假如我们现在有一个由
若现在有一个
那么我们就可以将一个
这样我们就把一个
由于
时间复杂度
提交记录。
QOJ9878. A xor B plus C
题意
给定四个数字
定义序列
求
题解
下文中使用
令
设
考虑
观察一下,可以发现这还能说明
首先来观察一下
那么还有
所以
同时我们也可以使用数学归纳法证明,所有
首先设
而
此外,还可以得到应该有
那么考虑一下这道题应该怎么做。
如果想要知道
但是若我们知道了
所以有一个自然的想法,就是我们去维护
根据前面的讨论,我们知道
令
那么后面的部分呢,我们仍然考虑暴力维护
如果
那么不妨假设
首先我们知道
如果
此时如果
这说明
同理,此时如果
那么说明
那么当
而根据我们的假设,
而这恰好又能推出
对于
那么根据我们之前的式子,此时就有
那么可以发现,这等价于
考虑令
先来考虑第一个条件,首先因为
那么
那么可以得到
那么就有
不妨设
那么考虑,
首先如果
否则
根据之前的证明,我们知道恰好存在一个
特殊的,从之前的证明还可以看出,所有的
那么若
这是好的,因为这部分情况下
而当
那么问题在于,
考虑如果
只有
所以此时应该有
那么去掉
对于
那么对于
所以说
设
令
那么在
然后用 set 瞎模拟一下每一个数字消失的时间,能做到
直接暴力模拟最坏是
提交记录。
QOJ9881. Diverge and Converge
题意
给定两棵
现在需要构造两个长为
然后会进行
第二棵树同理,要求每一次操作完之后,得到的仍然是两棵树。
题解
考虑归纳进行构造,那么
设两棵树分别为
并起来的图一共有
这说明图中至少存在一个点
那么
若
那么我们考虑第一步把这两条边交换,然后把
则
那么如果
设
那么我们令
则
不妨假设,在时刻
那么对于
那么考虑在
那么下一步的操作是交换一条边
手动模拟一下,可以发现这样是合法的。
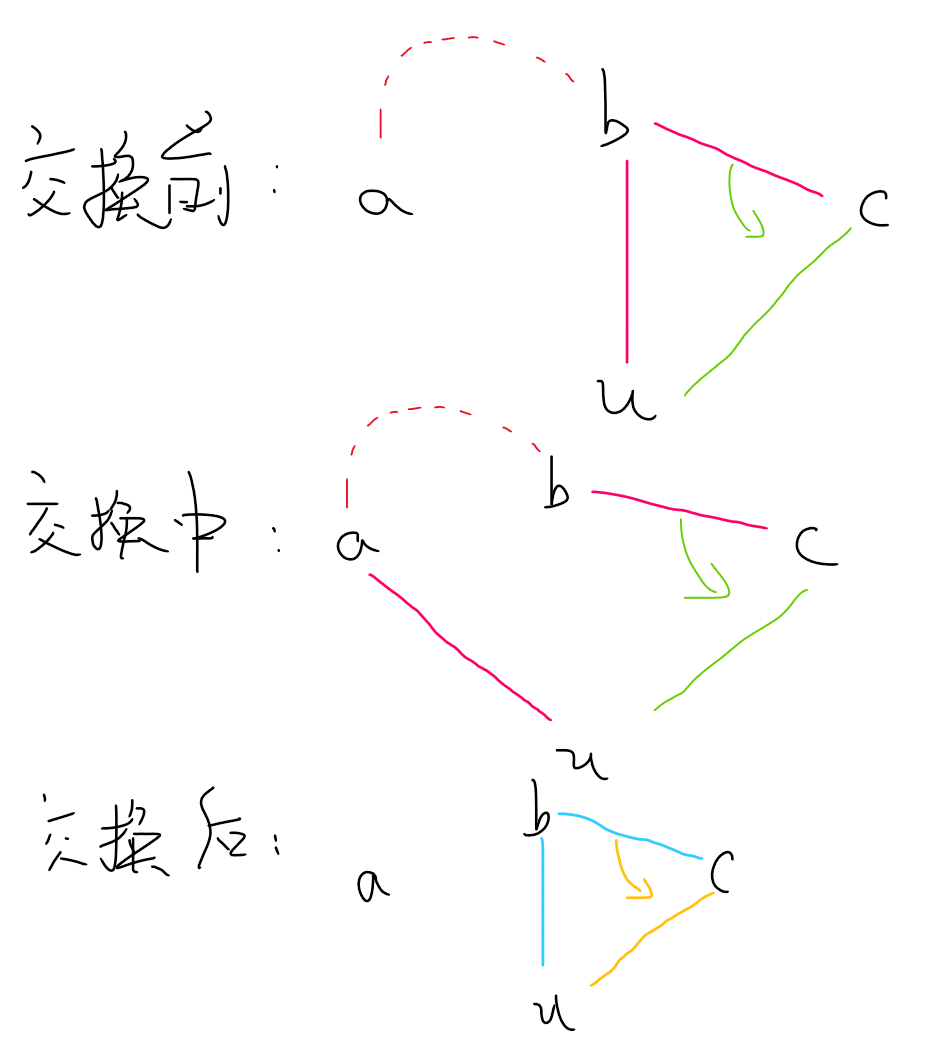
提交记录。
QOJ9882. Two Convex Sets
题意
给定二维平面上的
称一个点的集合是好的,当且仅当这个集合的每一个点,都不在集合凸包的内部(就是全在凸包上)。
求将整个点集划分为两个好的点集的方案数。
题解
先考虑,如果只让选出一个子集,使得选出的集合合法怎么做。
考虑枚举这个集合中,纵坐标最小的点
这样,剩余的所有点就全部在
由于我们枚举凸包上纵坐标最小的点为点
后面直接
然后依次考虑每一个点加不加入凸包,加入的话需要判断
最后统计答案的时候,如果
这样就能得到,如果只需要一个其中一个子集合法的方案数。
那么考虑原题怎么做,还是设纵坐标最小的点为
还是将剩下的点做极角排序,那么第二个凸包会被分成一个上凸壳和一个下凸壳。
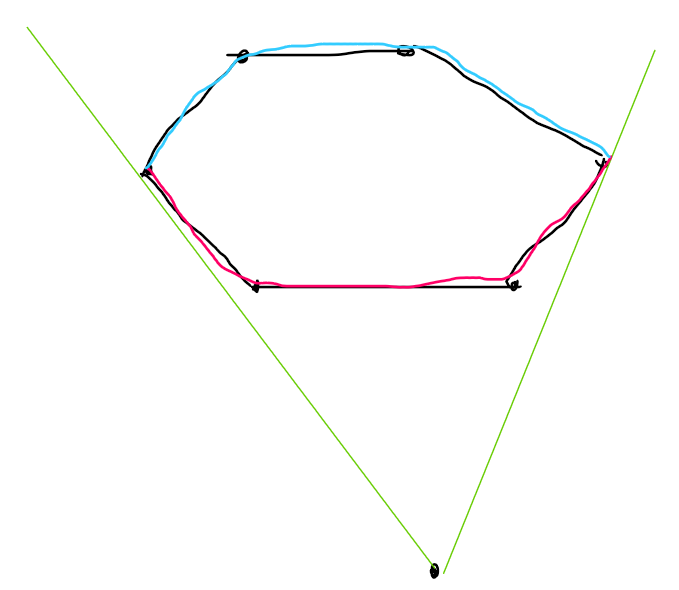
那么我们设
设
以及
转移的话直接对于
复杂度瓶颈显然在
那么考虑,
所以状态总数还是会小一点的,再考虑到大概率会有
仔细考虑感觉状态应该不会那么大,所以直接把
那么我们怎么知道这个哈希表到底需要开多大呢,考虑能让我们跑的最满的数据显然是
跑出来的结果说明,当
所有
提交记录。
QOJ9883. Near Pair
题意
给定三个数字
你进行一些询问,询问的方式是每一次给出一个集合
交互库将会回答,满足
设