too hard for me!
QOJ8807. Infiltration
题意
现在有一棵
在奇数时刻,Alice 可以选择走一步或者原地不动,偶数时刻 Bob 可以选择走一步或原地不动。
构造一组策略,令
构造的方案需要满足对于任意
输出策略的方式为,对于一个人和一个起点,输出所有时刻,这个人应该在哪个点。
题解
先考虑,如果两个人初始在一个数轴上,如何使他们相遇。
可以发现,先让 Alice 往右走
那么对于一条链的情况,相当于限制两人初始坐标在
考虑一个很无语的优化,我们取这条链的中点当作根,算出来恰好取得
那么放到树上,找到树直径的终点,然后以这个点为根,两个人轮流往上跳就好了。
由于未知的原因,输出策略时每一行后面都需要多输出一遍根,不然会挂。
提交记录。
QOJ9812. Binary Search
题意
现在有一个
称一个
判断是否存在不好的串,有的话输出最小长度。
题解
可以发现,最小的串一定是
使用反证法,假设当前最小的不好的串为
那么长度
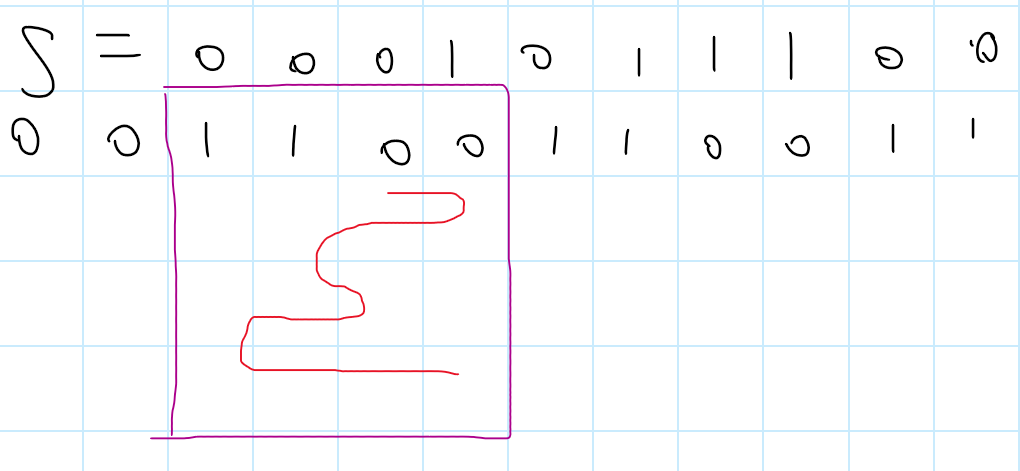
可以发现,一个串
也就是说,在上面这个图中,只需要
这与我们的假设冲突,所以最小的串一定是
那么这样就好办了,令
那么
提交记录。
QOJ8581. 섬
题意
给定一个正
现在可以进行若干次操作,每一次操作为选择一个三角形
进行最少次数操作,使得可以选出两个边不交的生成树(新加入的点也要连通)。
题解
先考虑不使用操作,此时有
如果使用一次操作,此时有
这个正
考虑以
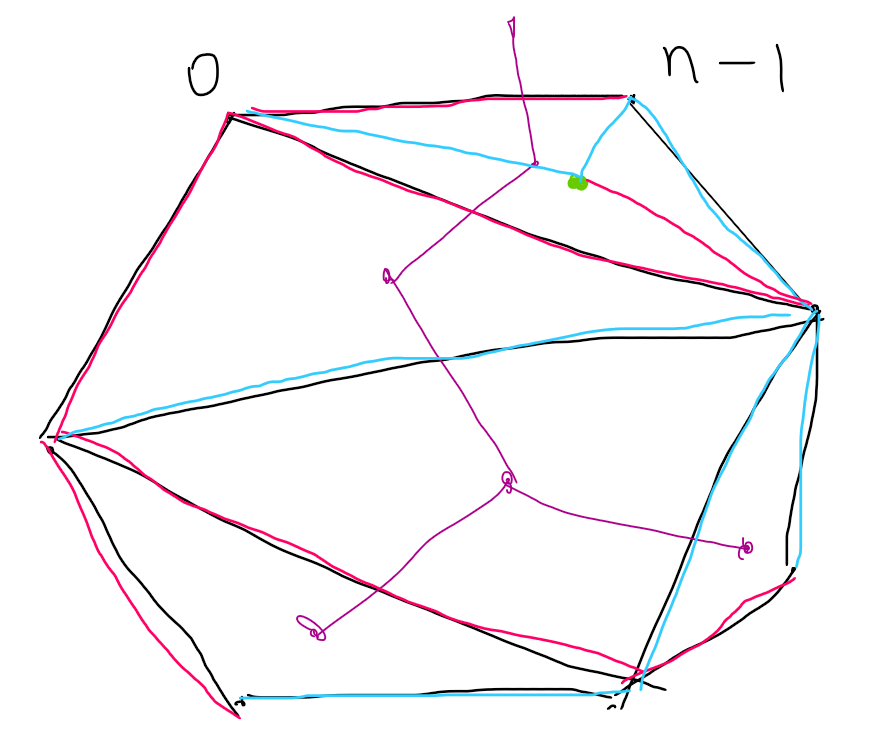
一个三角形,除了他和父亲连的那条边以外还有两条边。
那么把左右两条边分别分给第一个边集和第二个边集。
那么此时可以发现,红色边集除了
那么先把最上面一条边分给红色边集,这样红色边集就全部连通。
此时只有蓝色边集还存在两个连通块。
那么给
这样就成功搞出了两棵生成树。
提交记录。
QOJ9870. Items
题意
现在有
给一个
题解
令
可以发现,此时问题答案不变,但是
考虑对于一个合法方案,若前
那么若
若
这说明一定存在一个重量前缀和始终在
只保留
提交记录(不知道为啥保留
QOJ8577. 평균 최대화
题意
定义一个序列
一个序列
一次操作是选择一个封闭的连续子序列
给定一个长度为
题解
考虑哪些区间是封闭的。考虑建出整个序列的小根笛卡尔树。
可发现,若
如果满足这个条件可以发现,一定有
那么此时只需要额外要求
考虑一个询问
令
那么有
考虑用这个 dp 如何计算答案,显然求得是最大的
将所有的
考虑维护每一个区间对应的凸壳。
观察 dp 转移式,发现后面是一个
但是前面还有一个
所以需要一个手写的平衡树维护凸包上的点,加入新点的时候需要将前面若干个点进行合并。
询问时的
时间复杂度
提交记录。
(这题 spj 是唐诗,我怎么看别人直接返回
QOJ9863. Brackets
题意
给定一个长度为
额外给定
现在要求从
满足每一对的两个区间拼起来之后是合法括号串,且一个区间至多出现一次。
题解
考虑一个对
第一种情况是
第二种情况是
并且
分别统计这三类括号串的数量。
考虑什么括号串,可能在左右分别加入一些其他括号后变得合法。
可以发现,这种字符串,如果消掉中间已经匹配成功的部分,剩下的部分,一定是左边一段右括号,剩下的右边全是左括号。
那么一对合法的区间,在内部各自消完之前,应该大概长成
考虑分治来统计,以统计哪些字符串消完之后只剩下左括号举例。
尝试想象一下,在分治中心左右两侧,这个字符串可能长什么样子。
可以发现,可能大概长成这个样子,
中心的左侧一定没有右括号,并且中心右侧的右括号可以被左边的左括号全部消掉。
此时左侧剩余的左括号+右侧的左括号就是需要统计的部分。
提交记录。
QOJ9189. Make them Meet
题意
给定一个
现在可以进行若干轮操作,一轮操作是给每一个点染一个
然后两个人会走向一个,与当前点相邻,且颜色相同的点。没有这样的点则在原地不动,有多个则随机选一个走。
若某轮操作后两个人在同一个点,或者两个人经过了同一条边,则称两个人相遇了。
构造操作,使得无论两个人起点在哪里,中间过程选择了哪条边行走,他们中间都相遇过。
题解
首先从树看起,容易发现此时相当于是每一轮选择一些边激活。
但是树的情况仍然不好做,所以先来考虑链怎么做。
考虑奇数轮的时候让深度为奇数的边激活,偶数的时候让深度为偶数的边激活。
这样,一个人行走的路径,就是在从起点走到一个链头,然后在两个链头中间不断往返。
可以发现,走
再来考虑菊花怎么做。
考虑第一轮先让所有边激活,这样如果两个人初始在两个叶子,这一轮直接就相遇了。
否则,两人初始一个在叶子一个在根,一次操作之后肯定还是一个在叶子一个在根。
那么第二轮我们随便激活一条边,剩余的边关掉。
这样在根上的那个人就会走到那个叶子去,如果另一个人恰好在那个叶子上,两个人直接就相遇了。
否则,另一个人不会动,那么现在两个人就都在叶子上,直接再来一轮,激活所有边就好了。
这样可以在
最后考虑一个普通的树怎么做。
先来想能不能直接把链的做法套上来。
可以发现,这样是不行的,此时两个人的路径是在根和某个叶子直接晃,并且这个晃的叶子可能会更换。
此时可能会出现两个人一直晃但就不相遇的情况。
考虑再套一点点菊花的做法上来。
我们选择一个根的儿子,然后让根和这个儿子中间的边,一直被激活。
考虑这个时候一个人会怎么走。
对于大部分情况,一个人会(先向下走到某一个叶子,然后往上走,然后)一路走到根,然后持续在根和选择的儿子两个点中间一直晃。
但是还有特殊情况,可能会出现一个人初始在根和儿子中间来回晃,然后在某个时间突然逃逸,然后走到某个儿子再上来晃。
可以发现其实特殊情况不是很影响这个做法的正确性。考虑多少轮之后两个人会相遇。
最极限的情况应该是一个人初始在根和某个儿子中间晃,另一个人先走到一个叶子再往上走。
此时经过了
所以第二个人肯定在前
所以直接分析就会发现两个人肯定可以在
仔细思考还能得出,其实两人经过
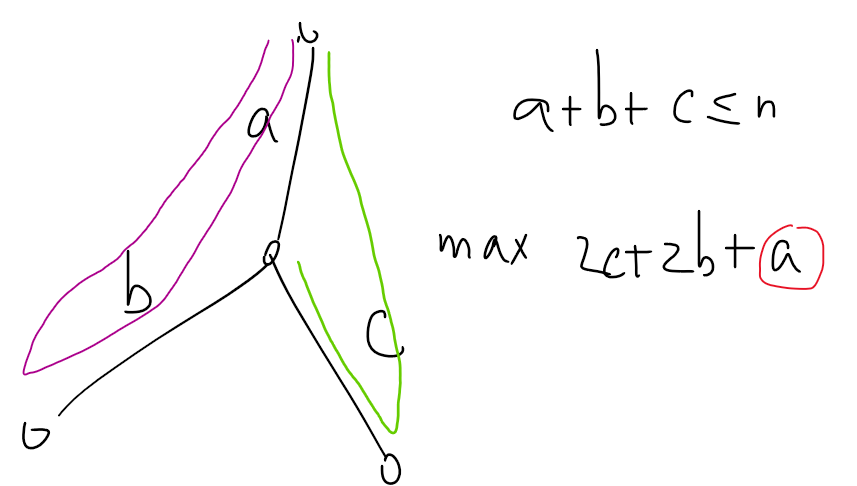
懒得证了自己看图吧。
这样我们就得到了树的做法。
再来考虑普通图怎么做。
一个很自然的想法是,能不能找出这个图的随便一棵生成树,然后套用树的做法。
思考可以发现,找到的生成树需要满足如下两个条件:
- 父亲相同的两个点,中间不能有边;
- 若在树的做法中,选出的根的儿子为
,则根和 的儿子之间不能有边。
首先第一个条件非常好满足,我们只需要找一棵 dfs 树即可,因为 dfs 树上没有横叉边。
那是否所有的图都能找到一个合适的根和
但是这个时候可以发现,完全图的 dfs 树是一条链,而这个时候是可以直接套用链的做法做的。
那么我们先找到这个图的随便一棵 dfs 树,用调整法搞出一个符合条件的图。
首先,如果这棵 dfs 树直接是一条链,那么直接套用链的做法。
否则这棵树一定存在“分叉点”,设最深的一个分叉点为
设
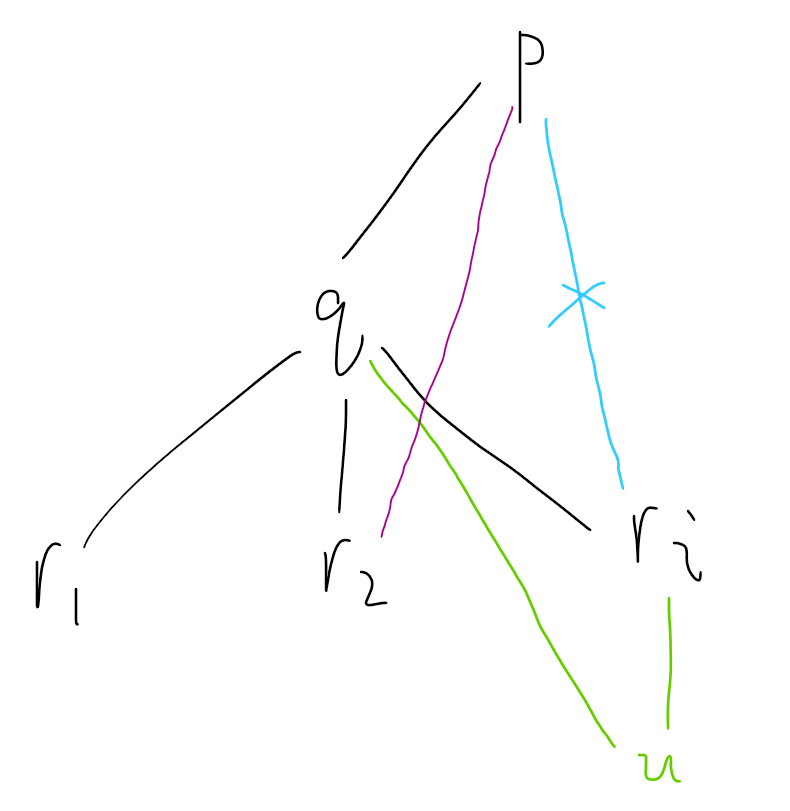
首先先把
然后以
考虑这样有什么好处,可以发现,如果
(需要注意的是,
那么令
然后我们将
(虽然还可能存在一些别的横叉边,但是这些边都不影响)。
考虑更改一下我们的操作,原来操作是一轮奇数边,一轮偶数边,一直反复。
现在加入一类操作,称为特殊边,在这一轮操作中,我们只让
现在我们让三种操作,奇数边,偶数边,特殊边一直反复。
(注意一下,这里奇数和偶数的操作由于深度定义不同,可能出现差异,所以正确的操作也可以能是先偶数边再奇数边)
如果这样操作的话,在原树上的人,行走路径不会改变。
在链上的人,会(先弹到底部,然后)走到
分析此时轮数,可以发现
此时还有一种情况,就是
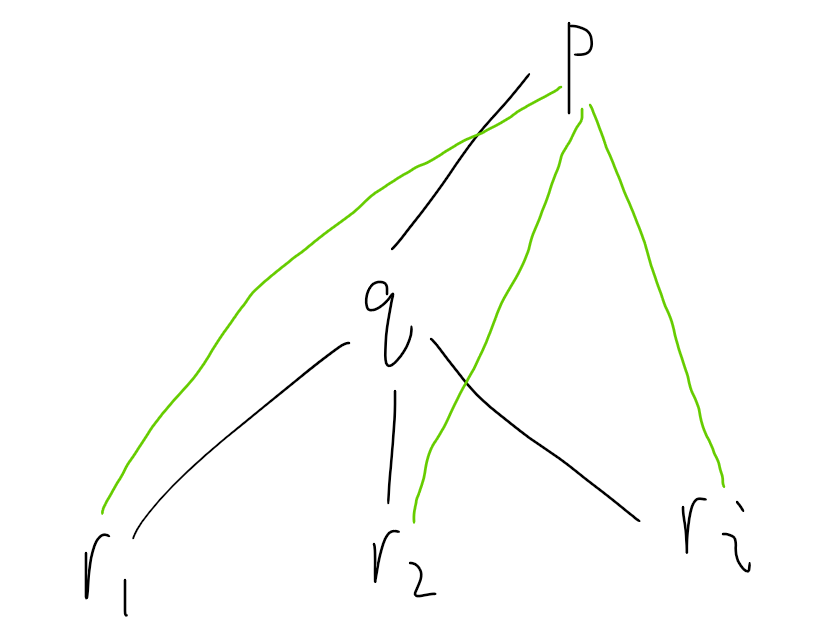
考虑直接拿
然后从
因为其他的
然后我们就构造出了和上面一种情况完全相同的生成树,和上面一样构造即可。
最终只需
我感觉这是对的啊不知道为什么 。
提交记录。
QOJ8578. 과일 게임
题意
现在有
一次合并操作为选择相邻两张牌使得
称一次游戏的结果为,进行若干次合并操作,最后拥有的等级最大的牌的等级。
进行
题解
先想静态的区间怎么做。
考虑按照等级从小到大的顺序,依次考虑每一个相同等级卡牌的连通块。
假设当前有一个等级为
因为我们是按照等级从小到大合成卡牌,所以这个块左右的卡牌都比这个块内要大。
也就是说块外怎么合并并不影响块内可以怎么合并。
考虑如果
否则
那么我们直接将这些牌变为,
这样一直合成下去,就能算出一个静态区间的答案了。
现在需要进行区间查询操作,优先考虑使用线段树进行维护。
但是直接维护显然是不行的,因为上述过程中我们要求卡牌按照等级从小到大进行合并,这肯定不能在线段树上做。
考虑一下为什么要求从小到大合并,原因是如果左右两边的卡牌都比他大,那么左右两侧不会影响中间的合并。
所以只需要某个块左右两边都比他大,就可以直接把这个块给合并,并不需要每一次找全局最小值合并。
这样的话,只要牌内部出现了凹下去的情况,我们就能把他合并掉。
所以合并完的结果,一定是一个凸起来的样子。
而卡牌最多就合成到
所以考虑,维护每一个区间合并成了什么样子。
两个区间合并的时候,直接暴力把两个子区间的结果拼一起然后暴力合并。
时间复杂度是
提交记录。
QOJ9185. Garden Decorations
题意
有
现在这些人想要搬家,原来住在
现在你可以进行若干次操作,对于第奇数次操作:
你将按照从
对于第偶数次操作,将按照
(输出策略时给定排列与当前的轮数,然后逐个给出经过的房子状态)
题解
考虑初始状态是一个向量
那么相当于是给定了一个满秩的矩阵
满足
那么初始令
考虑跑一个类似于高斯消元的东西,保证
考虑如果
由于
同理,
而现在我们需要利用这两种变换,把
考虑正常过程中我们怎么把一个矩阵消成下三角矩阵,流程如下:
- 对于
,首先在前 行中找一个第 列为 的行,然后把这一行和第 行换一下。 - 对于前
行里面第 列为 的行,用第 行给他异或一下把 消掉。
可以发现我们的操作用
考虑
那么直接用
这样就用消元的方法构造出了
提交记录。
(不知道为啥这题不能用快读)
还有一个 QOJ8195 我做过不写了。